interp1d
import numpy as np
from scipy import interpolate
import pylab as pl
x = np.linspace(0, 10, 11)
y = np.sin(x)
x_new = np.linspace(0, 10, 101)
pl.plot(x, y, 'ro')
for kind in ['zero', 'slinear', 'quadratic', 'cubic', 'linear', 'nearest', 'previous', 'next']:
f = interpolate.interp1d(x, y, kind=kind)
# f是一个函数，用这个函数就可以找插值点的函数值了：
y_new = f(x_new)
pl.plot(x_new, y_new, label=kind)
pl.legend(loc='lower right')
pl.show()
interp1d比Matlab的interp有些优势，因为返回的是函数，不需要在事先设定需要求解的点，而是在需要使用时调用函数。
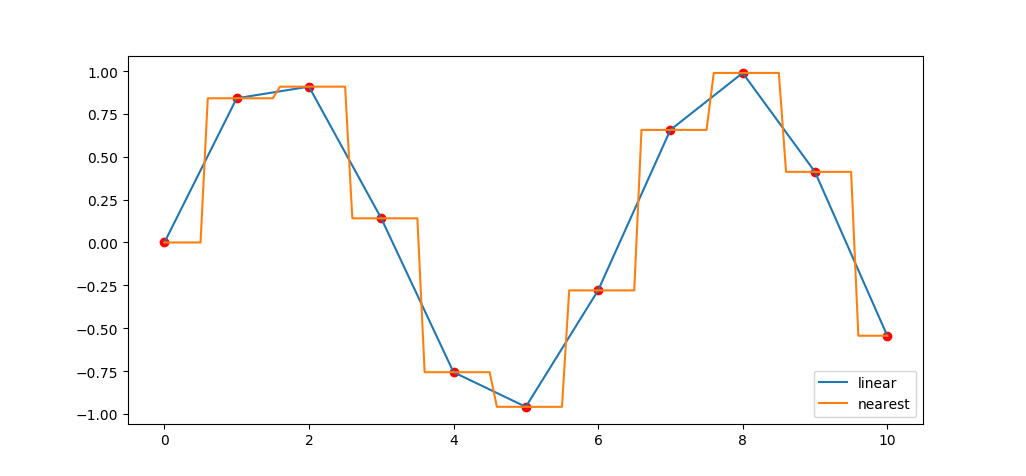
这个是linear和nearest的效果：
这个是zero, slinear, quadratic, cubic
也就是0, 1, 2, 3 次样条插值，所以这里的参数可以用str，也可以用数字
UnivariateSpline
interp1d不能外推运算（外插值）
UnivariateSpline可以外插值
调用方式如下：
UnivariateSpline(x,y,w=None,bbox=[None,None],k=3,s=None)
- x,y是X-Y坐标数组
- w是每个数据点的权重值
- k为样条曲线的阶数
- s为平滑参数。
- s=0，样条曲线强制通过所有数据点
- s>0,满足$\sum(w(y-spline(x)))^2 \leq s$
s=0强制通过所有数据点的外插值
from scipy import interpolate
import numpy as np
x1=np.linspace(0,10,20)
y1=np.sin(x1)
sx1=np.linspace(0,12,100)
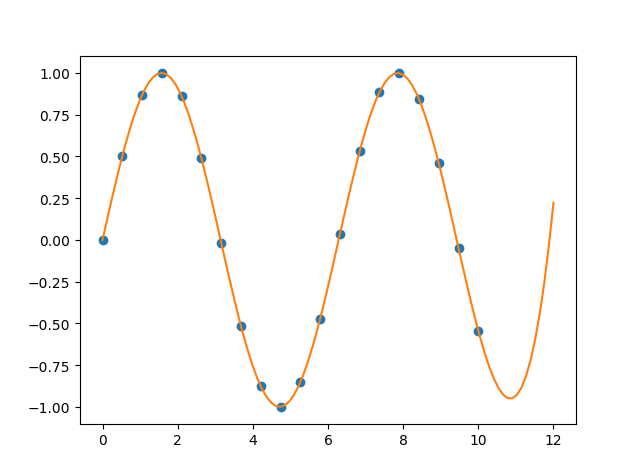
func1=interpolate.UnivariateSpline(x1,y1,s=0)#强制通过所有点
sy1=func1(sx1)
import matplotlib.pyplot as plt
plt.plot(x1,y1,'o')
plt.plot(sx1,sy1)
plt.show()
也就插值到(0,12)，范围再大就不行了，毕竟插值的专长不在于预测
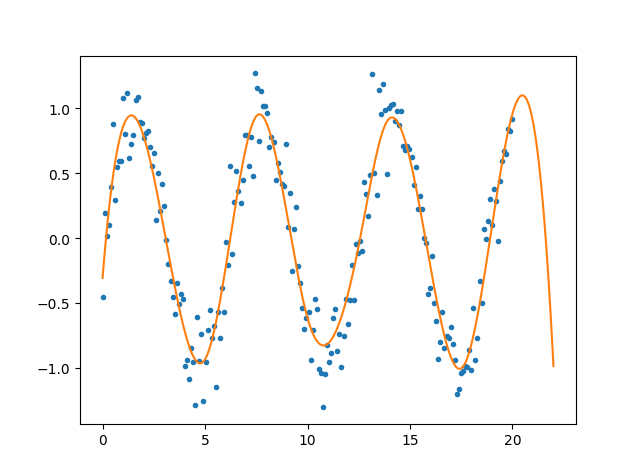
s>0：不强制通过所有点
import numpy as np
from scipy import interpolate
x2=np.linspace(0,20,200)
y2=np.sin(x2)+np.random.normal(loc=0,scale=1,size=len(x2))*0.2
sx2=np.linspace(0,22,2000)
func2=interpolate.UnivariateSpline(x2,y2,s=8)
sy2=func2(sx2)
import matplotlib.pyplot as plt
plt.plot(x2,y2,'.')
plt.plot(sx2,sy2)
plt.show()
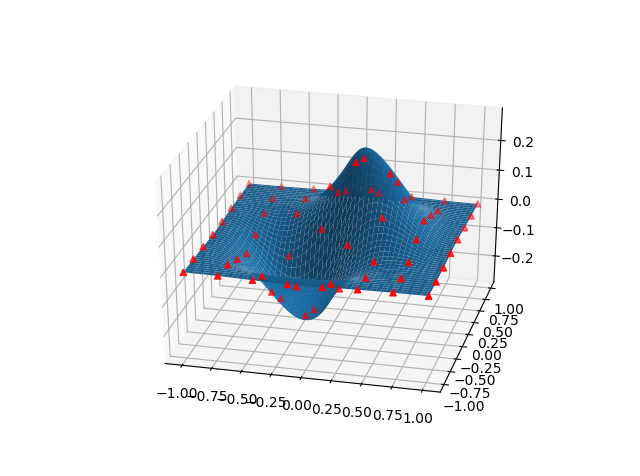
二维插值interp2d()
interp2d(x,y,z,kind='linear')
这里有几个注意事项：
- interp2d()中，输入的x,y,z先用ravel()被转成了一维数组
- func()的输入必须是一维的，输出是二维的（有点奇怪，感觉完成度不高）
- 插值的源数据必须是等距网格。不然的haul，运行不保存但结果不对。
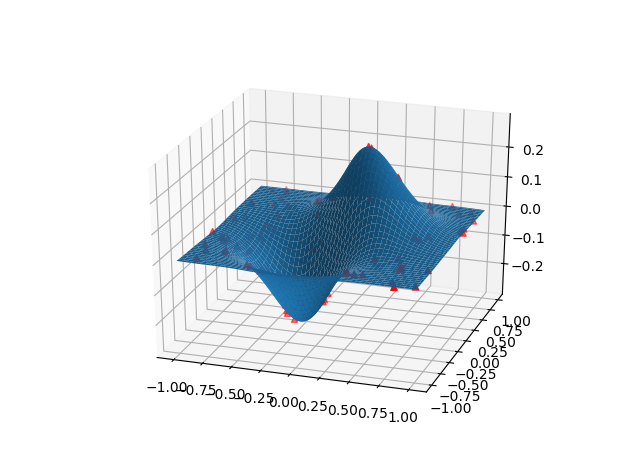
step1:生成数据
import numpy as np
def func(x,y):
return (x+y)*np.exp(-5*(x**2+y**2))
x,y=np.mgrid[-1:1:8j,-1:1:8j]
z=func(x,y)
step2:插值
from scipy import interpolate
func=interpolate.interp2d(x,y,z,kind='cubic')
xnew=np.linspace(-1,1,100)
ynew=np.linspace(-1,1,100)
znew=func(xnew,ynew)#xnew, ynew是一维的，输出znew是二维的
xnew,ynew=np.mgrid[-1:1:100j,-1:1:100j]#统一变成二维，便于下一步画图
step3:画图
import mpl_toolkits.mplot3d
import matplotlib.pyplot as plt
ax=plt.subplot(111,projection='3d')
ax.plot_surface(xnew,ynew,znew)
ax.scatter(x,y,z,c='r',marker='^')
plt.show()
二维插值Rbf()
Rbf的优点是，排列可以无序，可以不是等距的网格
step1:随机生成点，并计算函数值
import numpy as np
def func(x,y):
return (x+y)*np.exp(-5*(x**2+y**2))
x=np.random.uniform(low=-1,high=1,size=100)
y=np.random.uniform(low=-1,high=1,size=100)
z=func(x,y)
step2：插值
from scipy import interpolate
func=interpolate.Rbf(x,y,z,function='multiquadric')
xnew,ynew=np.mgrid[-1:1:100j,-1:1:100j]
znew=func(xnew,ynew)#输入输出都是二维
step3：画图
import mpl_toolkits.mplot3d
import matplotlib.pyplot as plt
ax=plt.subplot(111,projection='3d')
ax.plot_surface(xnew,ynew,znew)
ax.scatter(x,y,z,c='r',marker='^')
plt.show()
