【最小二乘估计】scipy.optimize.leastsq
🗓 2017年06月06日 📁 文章归类: 0x56_最优化
版权声明:本文作者是郭飞。转载随意,标明原文链接即可。
原文链接:https://www.guofei.site/2017/06/06/scipyleastsq.html
常见的曲线拟合
趋势模型里写了趋势模型中常用的10种曲线
这里是曲线拟合种常用的曲线
- Polynomial Models
$y=\sum\limits_{i=1}^{n} p_i x_i$ - Exponential Models
$y=ae^{bx},y=ae^{bx}+ce^{dx}$ - Fourier Series $y=a+\sum\limits_{i=1}^na_i \cos(nwx)+b_i \sin(nwx)$
- Gaussian Models
$y=\sum\limits_{i=1}^n a_i \exp(-(\dfrac{x-b_i}{c_i})^2)$ - Power Series
$y=ax^b,y=a+bx^c$ - Rational Polynomials
$y=\dfrac{\sum\limits_{i=1}^{n} p_i x_i}{\sum\limits_{i=1}^{n} q_i x_i}$ - Sum of Sines Models $y=a+\sum\limits_{i=1}^na_i \sin(nwx)$
- Weibull Distributions
$y=abx^{b-1}e^{-ax^b}$
widely used in reliability and life (failure rate) data analysis
leastsq
最小二乘估计原理是这样的:
$y=f(x,\theta)+\varepsilon$,
其中$\varepsilon$独立同分布。
$\theta=\arg\min \sum(y_i-f(x_i,\theta))^2$
非线性最小二乘法中,SST=SSR+SSE不再成立,但仍然可以定义R_squared=1-SSE/SST
leastsq可以用来做最小二乘估计,可以在线性拟合和非线性拟合中使用。
线性拟合案例
step1:生成模拟的源数据
import numpy as np
from scipy.optimize import leastsq
# 生成模拟数据
X=np.linspace(10,40,1000)
Y=0.8*X+2.1+np.random.normal(loc=0,scale=1,size=[1,1000])[0]
step2:定义残差并寻优
def residuals(p):
k,b=p
return Y-(k*X+b)
r=leastsq(residuals,[1,0])#[1,0]为初始值
k,b=r[0]
k,b
step3:计算误差
def S(k,b):
error=np.zeros(k.shape)
for x,y in zip(X,Y):
error+=(y-(k*x+b))**2
return error
S(k,b)
综合案例
step1:定义几个目标函数,准备一一检验其拟合效果
import numpy as np
def test_func1(x,p):
a,b=p
return a*x+b
def test_func2(x,p):
A,k,theta=p#这是一个编程技巧,虽然冗余了一行,但是可读性极大提高
return A*np.sin(2*np.pi*k*x+theta)
def test_func3(x,p):
a,b,c=p
return a*x**2+b*x+c
step2:定义目标函数和残差函数
p_true=[0.4,-2,0.9]#真实值
# 目标函数
def obj_func(x,p):
return test_func3(x,p)
# 残差
def residuals(p,y,x):
return y-obj_func(x,p)
step3:生成模拟数据
X=np.linspace(0,10,1000)
y=obj_func(X,p_true)+np.random.randn(len(X))
step4:拟合
from scipy.optimize import leastsq
p_prior=np.ones_like(p_true)# 先验的估计,真实数据分析流程中,先预估一个接近的值。这里为了测试效果,先验设定为1
plsq=leastsq(residuals,p_prior,args=(y,X))
print(p_true)
print(plsq)
step5:画图
import matplotlib.pyplot as plt
plt.plot(X,y)
plt.plot(X,obj_func(X,plsq[0]))
plt.show()
下面这3个目标函数拟合效果的展示:
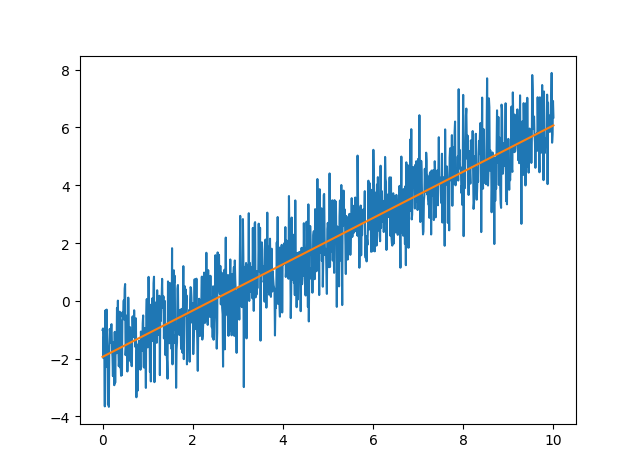
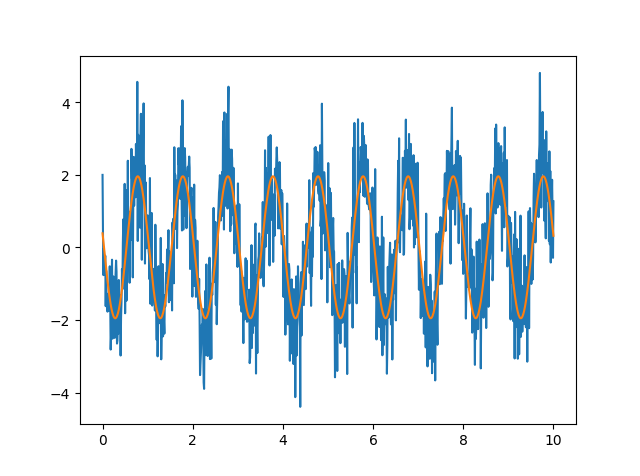
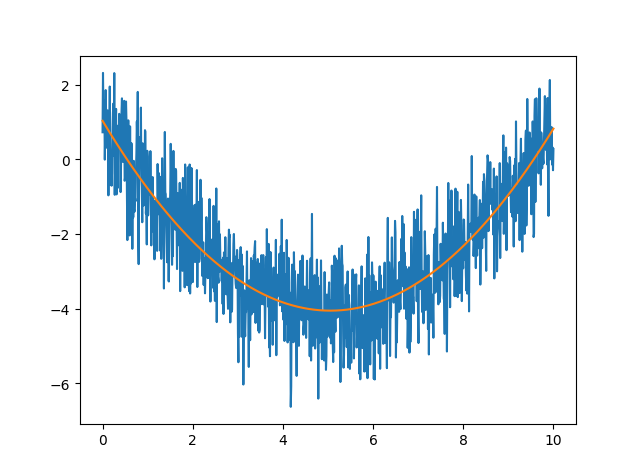
您的支持将鼓励我继续创作!
