模型介绍
条件随机场(conditional random field， CRF)1
与其他模型的关系
每一个HMM模型都等价于某个CRF2
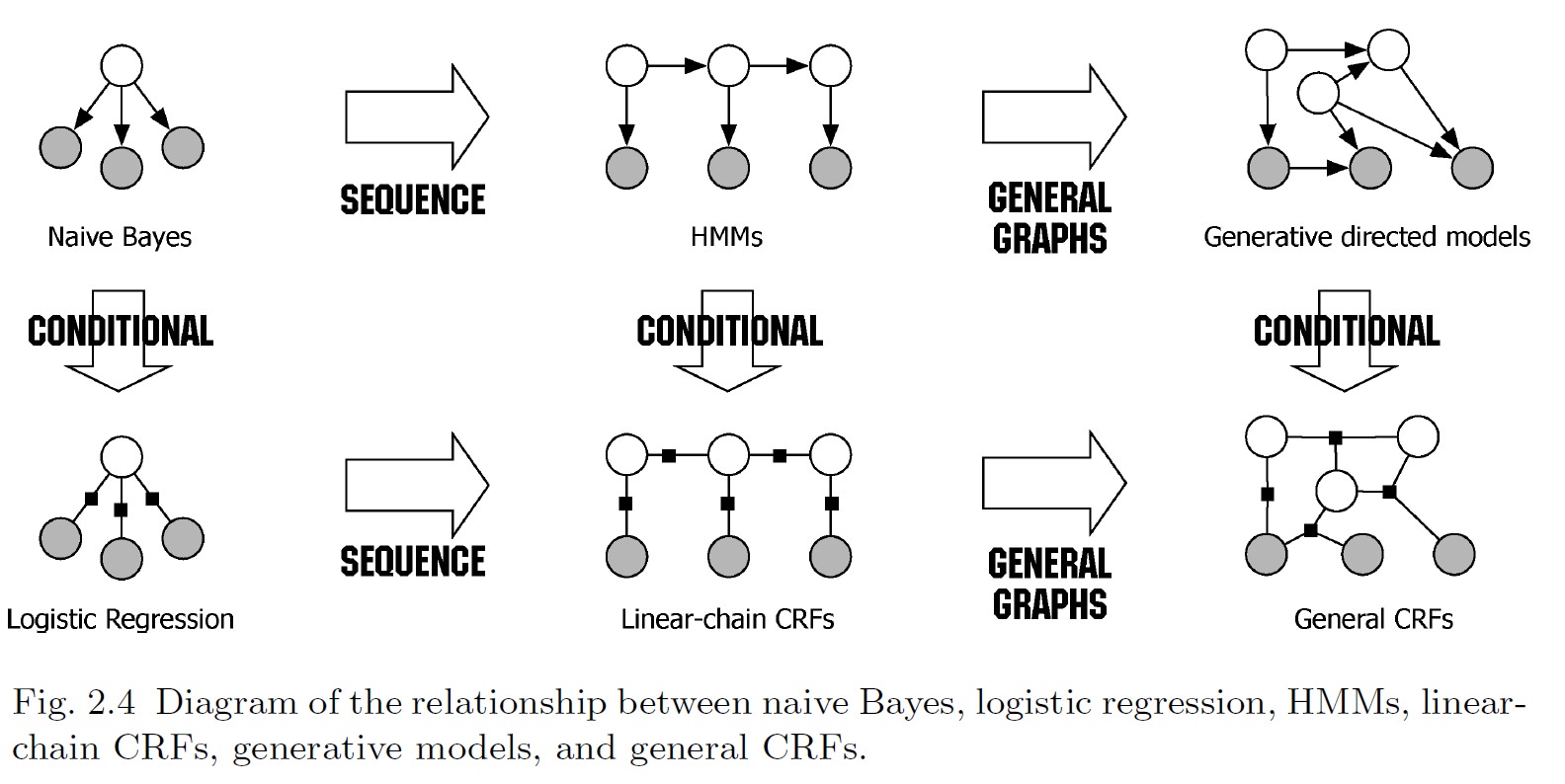
概率图分为两类：
- 有向图。（贝叶斯网络，信念网络）3
- 无向图。（马尔科夫随机场，马尔科夫网络）
基础定义
概率图模型(probabilistic graphical model)用graph表示概率分布。4
在无向图$G=(V,E)$上，每个节点$v\in V$对应一个随机变量$Y_v$，每个边$e\in E$对应随机变量之间的关系。
进而定义三个概念：
- 成对马尔科夫性(pairwise Markov property)
- 局部马尔科夫性(local Markov property)
- 全局马尔可夫性(global Markov property)
- 成对马尔科夫性
- $u,v$是无向图G上任意两个不相邻的结点，其它所有结点是O.$P(Y_u,Y_v\mid Y_O)=P(Y_u\mid Y_O)P(Y_v\mid Y_O)$
- 局部马尔可夫性
- $v$是G上一个结点，$W$是与$v$相连的所有结点，$O$是$v,W$外的所有结点。$P(Y_v,Y_O\mid Y_W)=P(Y_v\mid Y_W)P(Y_O\mid Y_W)$
- 全局马尔可夫性
- $A,B,C\subset V$是点集，A,B被C分开。$P(Y_A,Y_B\mid Y_C)=P(Y_A\mid Y_C)P(Y_B\mid Y_C)$
实际上，成对马尔科夫性、局部马尔可夫性、全局马尔可夫性是等价的。
一个概率图模型 ，如果满足马尔可夫性（成对、局部、全局），叫做 概率无向图模型（probability undirected graphical model），或者 马尔科夫随机场（Markov random field）
因子分解
C是无向图G的子图，如果C是完全图，叫做一个 团(clique)。
如果一个团不能再加入任何一个结点，叫做 最大团（maximal clique）
给定概率无向图模型，可以分解成所有 最大团 C的乘机形式，也就是说$P(Y)=\dfrac{1}{Z}\prod\limits_C \Psi_C(Y_C)$,
其中，Z是规范化因子$Z=\sum\limits_Y\prod\limits_C\Psi_C(Y_C)$
其中，$\Psi(Y_C)$称为势函数，势函数是严格正函数。
（通常，可以这么定义$\Psi_C(Y_C)=\exp(-E(Y_C))$）
Hammersley-Clifford定理：对于任意概率无向图，都可以做上述因子分解。
