竞争神经网络&LVQ
🗓 2017年12月12日 📁 文章归类: old_ann
版权声明:本文作者是郭飞。转载随意,标明原文链接即可。
原文链接:https://www.guofei.site/2017/12/12/competitive.html
关键词:
竞争神经网络
WTA学习法则
自组织竞争神经网络是一种无监督学习算法
竞争神经网络
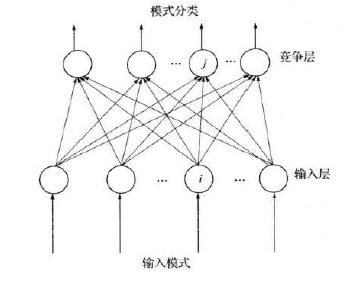
输入层记为第I层,输出层记为第J层
1. 归一化
$\hat X =\dfrac{X}{\mid \mid X \mid \mid}, \hat W_j=\dfrac{W_j}{\mid\mid W_j\mid\mid}$
2. 寻找获胜神经元
寻找获胜神经元,编号为$j^* $
所谓获胜神经元,指的是 最相似 的神经元。
最相似神经元的编号j满足\(j^* =\arg\min\limits_{j\in \{1,2,...n\}}\mid\mid\hat X-\hat W_j\mid\mid\)
又因为$\mid\mid \hat X-\hat W_j\mid\mid=\sqrt {(\hat X-\hat W_j)(\hat X-\hat W_j)^T}=\sqrt{2(1-\hat W\hat X^T)}$
所以,最相似 的神经元等价于使得$\hat W\hat X^T$最大的神经元
所以,只需要寻找\(j^* =\arg\max\limits_{j\in \{1,2,...n\}}\hat X \hat W_j^T\)
3. 网络输出
根据WTA学习规则(Winner Takes All),获胜神经元输出1,其它神经元输出0
即:\(y_j(t+1)=\left \{ \begin{array}{ccc}
1&j=j^* \\
0&j\neq j^*
\end{array}\right.\)
4. 权值调整
只有获胜的神经元才调整权值
即\(W_j(t+1)=\left \{ \begin{array}{ccc}
\hat W_j(t)+\Delta W_j=\hat W_j(t)+\alpha(\hat X-\hat W_j) &j=j^* \\
W_j(t)&j\neq j^*
\end{array}\right.\)
其中,$\alpha$是学习率,随着学习的进展,逐渐趋近于0
这样的学习规则下,权重始终满足这个性质:
$\mid\mid W_j \mid\mid=1$(简单列式可以证明)
其它trick
整个学习过程中,可能出现这种情况:
某些神经元从头到尾都没有竞争胜出,叫做 死神经元 。如果死神经元过多的话,分类不够精细。
采用这种策略:每次迭代中,对于那些从未胜出的神经元,设定一个较大的bias,使得这些神经元更加可能胜出,一旦曾经胜出,就把bias设为正常值。
代码实现
(应当先做 train-test 分离,这里没做)
from sklearn import datasets, metrics
import numpy as np
# 生成聚类算法数据集
X, y_true = datasets.make_blobs(
n_samples=1000,
n_features=2,
centers=3,
center_box=(-1, 1), # 取值范围
cluster_std=0.05,
random_state=23)
def normalization(inp: np.ndarray):
# 归一化,使其每一行的 L2-norm = 1
return inp / np.sqrt(np.square(inp).sum(axis=1, keepdims=True))
class CompetitiveNeuralNetwork:
def __init__(self, n1, n2, alpha=0.02):
self.n1 = n1 # 输入层的神经元个数,等于 feature 数量
self.n2 = n2 # 竞争层的神经元个数,等于输出的类的个数
self.w = normalization(np.random.randn(n2, n1)) # 初始化权重
self.a = alpha # 学习率
def train(self, X, max_iter=2000):
X = normalization(X)
n_sample = X.shape[0]
for i in range(max_iter):
k = np.random.randint(n_sample)
one_data = X[[k], :]
out = self.w @ one_data.T
ind = out.argmax()
self.w[ind, :] = self.w[ind, :] + self.a * (one_data[0, :] - self.w[ind, :])
# 这里需要对 w 做归一化,否则 w 会逐渐变小,但实际上少量迭代仍然能保证 |w| ≈ 1
def predict(self, X):
score = X @ self.w.T
ind = score.argmax(axis=1)
return ind
competitive_nn = CompetitiveNeuralNetwork(n1=X.shape[1], n2=3)
competitive_nn.train(X, max_iter=2000)
y_predict = competitive_nn.predict(X)
# %%
# ARI = 0 表示结果随机,ARI = 1 表示完全正确
print('ARI=', metrics.adjusted_rand_score(y_true, y_predict))
LVQ
学习矢量量化(Learning Vector Quantization, LVQ),于1988年由Kohonen提出的 有监督学习 算法,
根据各种改进版本,分为 LVQ1、LVQ2和LVQ3,其中 LVQ2 的应用最为广泛和有效。
LVQ1 每次只更新最胜出的1个神经元,LVQ2又引入了 次获胜 神经元,这里只写LVQ2的算法步骤,LVQ1更加简单一些。
LVQ2的算法步骤
输入:
数据集 \(D=\{ (x_1, y_1), (x_2, y_2),...,(x_m, y_m)\}\);
类别个数为q
神经元中的向量(叫做 原型向量 )\(\{p_1, p_2,..., p_q\}\)
学习率$\eta\in(0,1)$
学习过程
step1:输入一个样本x,计算它到每个原型向量的距离
step2:在这些距离中,找到最小的两个,标号i,j(距离本身定义为$d_i, j_j$)
step3:(一堆if,分开写)
如果最近的两个距离,其值差不多(定义为\(\min \{\dfrac{d_i}{d_j}, \dfrac{d_j}{d_i}\}>\rho\))那么,跳到step4(LVQ2更新规则),否则跳到step5(LVQ2更新规则)
step4(LVQ2更新规则):
如果i的类别正确,$w_i:=w_i+\eta(x-w_i), w_j:=w_j-\eta(x-w_j)$
如果j的类别正确,$w_i:=w_i-\eta(x-w_i), w_j:=w_j+\eta(x-w_j)$
跳到step1,进行下一步循环
step5(LVQ更新规则):
如果i标签正确$w_i:=w_i+\eta(x-w_i)$
如果i标签不正确$w_i:=w_i-\eta(x-w_i)$
LVQ的缺点
- 有可能不收敛。想象数据中有错误的标签,权重会一直来回跳动。
- 各个维度重要性一样。这个问题来自使用的是欧氏距离。
LVQ的应用
Matlab提供了实现
newlvq
learnlvq, learnlvq2
应用的话,找到两个
- 乳腺癌诊治。典型的一个有监督问题。
- 人脸朝向识别。输入数据需要用其它算法或人工把眼睛位置特征提取出来,然后人脸朝向是5个类别。也是典型的有监督问题。(更新这部分是2020年,这个应用已经完成历史使命了)
参考文献
《神经网络原理及应用》朱大奇,史慧,科学出版社
《人工神经网络理论及应用》韩立群,机械工业出版社
《Matlab神经网络原理与实例精解》陈明,清华大学出版社
《神经网络43个案例》王小川,北京航空航天大学出版社
《人工神经网络原理》马锐,机械工业出版社
额外
网上的竞争神经网络
x=[4.1,1.8,0.5,2.9,4.0,0.6,3.8,4.3,3.2,1.0,3.0,3.6,3.8,3.7,3.7,8.6,9.1,7.5,8.1,9.0,6.9,8.6,8.5,9.6,10.0,9.3,6.9,6.4,6.7,8.7];
y=[8.1,5.8,8.0,5.2,7.1,7.3,8.1,6.0,7.2,8.3,7.4,7.8,7.0,6.4,8.0,3.5,2.9,3.8,3.9,2.6,4.0,2.9,3.2,4.9,3.5,3.3,5.5,5.0,4.4,4.3];
data=[x;
y];
%%
[dataone]=mapminmax(data);
x=dataone(1,:);
y=dataone(2,:);
%%
w=rand(2,2);
sigma=0.2;
maxiterator=2000;
%%
for i=1:maxiterator
k=randi(30);
ds=dataone(:,k);
out=w*ds;
[~,ind]=max(out);
w(ind,:)=w(ind,:)+sigma*(ds'-w(ind,:));
end
%%
plot(x,y,'.')
hold on
plot(w(:,1),w(:,2),'o')
自己写的代码
from sklearn import datasets
import numpy as np
data, target = datasets.make_blobs(n_samples=100, n_features=2, centers=3, center_box=(-1, 1), cluster_std=0.05,
random_state=23)
import matplotlib.pyplot as plt
plt.plot(data[:, 0], data[:, 1], '.')
# plt.show()
sample_counts, N = data.shape # sample个数, 输入层个数
M = 3 # 竞争层个数
w = np.random.rand(M, N)
# w=np.random.rand(2,2)
a = 0.02 # 学习率
max_iter = 200000
data = data.T
for i in range(max_iter):
k = np.random.randint(sample_counts)
one_data = data[:, [k]]
out = np.dot(w, one_data)
ind = out.argmax()
w[ind, :] = w[ind, :] + a * (one_data.T - w[ind, :])
plt.plot(w[:, 0], w[:, 1], 'o')
plt.show()
您的支持将鼓励我继续创作!
