【fft】傅立叶变换
🗓 2018年01月06日 📁 文章归类: 0x53_复变与积分变换
版权声明:本文作者是郭飞。转载随意,标明原文链接即可。
原文链接:https://www.guofei.site/2018/01/06/fourier.html
傅立叶展开
函数系
考察函数系:
$1, \cos t, \sin t,\cos 2t, \sin 2t, …, \cos nt, \sin nt,…$
这个函数系有一个性质 “正交性” ,任意两个不同的函数乘积在$[-\pi,\pi]$上的积分都是0.
- 卷积
- $\int_{-\infty}^{+\infty}f_1(\tau)f_2(t-\tau)d\tau$
傅立叶级数的三角形式
- 狄利克雷条件
-
- 连续或只有有限个第一类间断点。2. 只有有限个极值点。
周期为$T$的周期函数$f(t)$,如果满足狄利克雷条件,就可以表示为:
$f(t)=\dfrac{a_0}{2}+\sum\limits_{n=1}^{+\infty}(a_n\cos n wt+b_n \sin nwt)$
其中,$w=\dfrac{2\pi}{T}$
$a_0=\dfrac{2}{T}\int_{-T/2}^{T/2} f(t) dt$
$a_n=\dfrac{2}{T}\int_{-T/2}^{T/2} f(t)\cos nwt dt$
$b_n=\dfrac{2}{T}\int_{-T/2}^{T/2} f(t)\sin nwt dt$
(被称为 欧拉-傅立叶公式)
(可以由函数系的 正交性 推导出来)
性质
如果$f(t)$是偶函数,那么$b_n=0$
如果$f(t)$是奇函数,那么$a_n=0$
傅立叶级数的复指数形式
考虑到
$\cos nwt=\dfrac{1}{2}(e^{inwt}+e^{-inwt})$
$\sin nwt=\dfrac{1}{2}(e^{inwt}-e^{-inwt})$
得到
$f(t)=\dfrac{a_0}{2}+\sum\limits_{n=1}^{+\infty}(\dfrac{a_n-ib_n}{2}e^{inwt}+\dfrac{a_n+ib_n}{2}e^{-inwt})$
所以傅立叶变换也可以写为:
$f(t)=\sum\limits_{n=-\infty}^{+\infty}c_ne^{inwt}$
其中,$c_n=\dfrac{1}{T}\int_{-T/2}^{T/2}f(t)e^{inwt}dt(n=0,\pm1,\pm2,…)$
三角形式
令$A_0=a_0/2,A_n=\sqrt{a_n^2+b_n^2},\cos \theta_n=a_n/A_n,\sin\theta_n=\dfrac{-b_n}{A_n}$
那么,
$f(t)=A_0+\sum\limits_{n=1}^{+\infty}A_0\cos(nwt+\theta_n)$
$A_n$称为 振幅 ,$\theta_n$表示 相位
复指数形式中,$\mid c_n \mid=\mid c_{-n} \mid =A_n/2$就是振幅谱,$\arg c_n=-\arg c_{-n}=\theta_n$就是相位谱
傅立叶变换
连续傅立叶变换
当T增大时,$w=2\pi/T$越来越小,意味着频率的间隔越来越小;当$T\to+\infty$,频谱将变成一个连续值,现在我们分析这种情况
$f(t)=\lim\limits_{T\to+\infty}f_T(t)$
$=\dfrac{1}{2\pi}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}f(\tau)e^{-iwt}d\tau]e^{iwt}dw$
- 傅立叶变换
- $F(w)=\int_{-\infty}^{+\infty} e^{-iwt} f(t) dt$
- 傅立叶逆变换
- $f(t)=\dfrac{1}{2 \pi} \int_{-\infty}^{+\infty} e^{iwt}F(w)dw$
有教材的另一种写法
- 傅立叶变换
- $F(w)=\int_{-\infty}^{+\infty} f(t) e^{-i2\pi wt} dt$
- 傅立叶逆变换
- $f(t)=\dfrac{1}{2 \pi} \int_{-\infty}^{+\infty} e^{i2\pi wt}F(w)dw$
$F(w)$是频谱密度函数,$\mid F(w)\mid$是振幅谱,$\arg F(w)$是相位谱
th
如果:
$f(t)$是周期函数
那么,
$f(t)$可以表示为$f(t)=\sum\limits_{n=-\infty}^\infty C_n e^{-i\pi n t/p}$
$\delta$函数
- $\delta$函数(单位冲击函数,狄拉克函数,Dirac)
- 满足这两个条件的函数: 1) \(\delta(t)= \left \{ \begin{array}{c} 0& t\neq 0 \\ \infty & t=0\end{array}\right.\) 2) $\int_{-\infty}^{+\infty}\delta(t)dt=1$
以上定义并不是严格定义,而是一种直观描述,$\delta$函数并不是经典意义上的函数,而是一种广义函数。
性质1
$f(t)$在R上有界,在$t=0$处连续,那么,
$\int_{-\infty}^{+\infty}\delta(t)f(t)dt=f(0)$
性质1又称为取样(sifting)特性
也可以写为 $\int_{-\infty}^{+\infty}f(t)\delta(t-t_0)dt=f(t_0)$
性质2
$\delta(t)=\delta(-t)$ (偶函数)
性质3
设$u(t)$为单位阶跃函数,即\(u(t)=\left\{\begin{array}{l}1,t>0\\0,t<0 \end{array}\right.\),那么有,
$\int_{-\infty}^t\delta(t)dt=u(t),\dfrac{d[u(t)]}{dt}=\delta(t)$
性质4
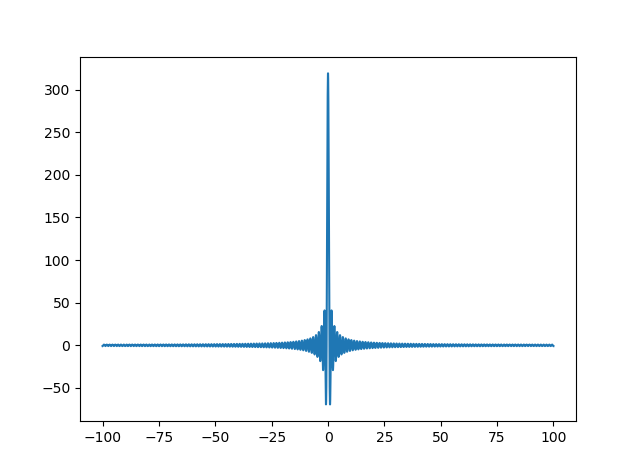
$\mathscr F(\delta(t))=1,\mathscr F^{-1}(1)=\delta(t)$
关于性质4,用$F(w)=1$画出形象示意图如下:
# dirac函数的傅立叶性质
# F(1)=\delta(t)的形象表示
import numpy as np
import matplotlib.pyplot as plt
w_list = np.arange(start=-5, stop=5, step=np.pi / 100) # step定为一个无理数,最大程度模拟连续型w
x = np.arange(start=-100, stop=100, step=0.01)
y_sum = np.zeros_like(x)
for w in w_list:
y = 1 * np.cos(w * x)
y_sum += y
plt.plot(x, y_sum)
plt.show()
傅立叶变换的性质
- 线性性质
若$F(w)=\mathscr F(f(t)),G(w)=\mathscr F(g(t))$,那么,
$\mathscr F(af(t)+bg(t))=aF(w)+bG(w)$
$\mathscr F^{-1}(aF(t)+bG(t))=af(t)+bg(t)$ - 位移性质
若$F(w)=\mathscr F(f(t)),t_0,w_0$是实常数,那么
$\mathscr F(f(t-t_0))=e^{-iwt_0}F(w)$
$\mathscr F^{-1}(F(w-w_0))=e^{iw_0t}f(t)$ - 相似性
若$F(w)=\mathscr F(f(t)),a$是非0常数,那么
$\mathscr F(f(at))=\dfrac{1}{\mid a\mid}F(\dfrac{w}{a})$ - 微分性质
若$\lim\limits_{\mid t\mid \to +\infty}f(t)=0$,那么
$\mathscr F(f^{(n)}(t))=(iw)^n \mathscr F(f(t))$
$\dfrac{d^n F(w)}{dw^n}=(-i)^n \mathscr F(t^nf(t))$ - 积分性质
设$g(t)=\int_{-\infty}^tf(t)dt,\lim\limits_{t\to+\infty}g(t)=0$,那么,
$\mathscr F[f(t)]=\mathscr F[g’(t)]=iw\mathscr F[g(t)]$ - 帕塞瓦尔(Parseval)等式
设$F(w)=\mathscr F(f(t))$,那么
$\int_{-\infty}^{+\infty}f^2(t)=\dfrac{1}{2\pi}\int_{-\infty}^{+\infty} \mid F(w)\mid^2dw$
离散傅立叶变换
如果:
${ f_0,f_1,…f_{N-1} }$ 满足 $\sum\limits_{n=0}^{N-1} \lvert f_n \rvert <\infty$
傅立叶变换: $X(k)=F(f_n)=\sum\limits_{n=0}^{N-1} f_n e^{-i \dfrac{2 \pi k}{N} n}$
傅立叶逆变换: $f_n=\dfrac{1}{N} \sum\limits_{k=0}^{N-1} X(k) e^{i \dfrac{2 \pi k}{N} n}$
冲击函数
离散系统中,也可以定义冲击函数 \(\delta(t)= \left \{ \begin{array}{c} 0& t\neq 0 \\ 1 & t=0\end{array}\right.\)
然后,可以得到与连续系统一致的性质
- $\sum\limits_{x=-\infty}^\infty \delta(x)=1$
- $\sum\limits_{x=-\infty}^\infty f(x)\delta(x)=f(0)$
- $\sum\limits_{x=-\infty}^\infty f(x)\delta(x-x_0) = f(x_0)$
卷积
卷积是一种算子,定义为
$f(t) \ast h(t)=\int_{-\infty}^\infty f(\tau)h(t-\tau)d\tau$
直观理解:把一个函数做翻转,然后划过另一个函数。滑动过程中每个位移处执行乘积之和。
TH1:卷积可交换,就是 $f \ast g = g \ast f$
定理:如果$f(t),h(t)$的傅立叶变换是$F(u),H(u)$,那么卷积 $f(t) \ast h(t)$ 的傅立叶变换是 $F(u)H(u)$
- 用各自的定义去推导,用到一个积分交换,不难。
- 换句话说,两边可以相互获得 $f(t)\ast h(t) \Leftrightarrow F(u)H(u)$
- 定理还有另一半。$f(t)h(t)\Leftrightarrow F(u)\ast H(u)$
取样
取样。用计算机处理之前,需要把连续函数转换成离散的序列。用语言描述取样,实际上是每隔一个间隔,取函数值。
数学表示: $f_k=\int_{-\infty}^\infty f(t) \delta(t-k\Delta T) dt=f(k\Delta T)$
如果取样后的结果记为$\tilde f$,对应傅立叶变换为$\tilde F$,
- $\tilde f=f(t)s_{\Delta T}(t)$
- 根据卷积定理$\tilde F=F(u)\ast S(u)$
- $S(u)$事先可以算出来$S(u)=\dfrac{1}{\Delta T}\sum\limits_{n=-\infty}^\infty \delta(u-\dfrac{n}{\Delta T})$
- 取样定理
- 如果以超过函数最高频率的两倍的取样率来获取样本,连续的带限函数可以完全从它的样本集中恢复。
还有一些结论:连续函数 $f$ 的取样是 $\tilde f$,对应的傅立叶变换 $F$ 的取样是 $\tilde F$,
那么把取样后的函数当成离散数列,恰好对应离散傅立叶变换 $\tilde F(u)=\sum\limits_{n\to -\infty}^\infty f_n \exp{(-j2\pi un\Delta T)}$
(其实不是恰好,而是说离散傅立叶变换就是这么定义的)
二维傅立叶变换
推广
定义连续二维冲击函数
\(\delta(t,z)=\left \{ \begin{array}{cc}\infty & t=z=0\\
0 & o/w
\end{array}\right.\)
并且
$\int_{-\infty}^\infty \int_{-\infty}^\infty \delta(t,z)dtdz=1$
然后有一系列类似一维的性质,不多说。
二维傅立叶变换:
$F(u,v)=\int_{-\infty}^\infty \int_{-\infty}^\infty f(t,z)\exp{(-j2\pi (ut+vz))} dtdz$
二维傅立叶逆变换:
$f(t,z)=\int_{-\infty}^\infty \int_{-\infty}^\infty F(u,v) \exp{(j2\pi (ut+vz))} dudv$
二维傅立叶变换也有对应的 取样定理,不多说。
关于采样,(在数字图像处理中),同样衍生处 混淆 的概念。
- 一维混淆。包括空间混淆和时间混淆。都是欠取样造成的。
- 空间混淆。例如线装特征中的锯齿、伪高光、原图像不存在的模式
- 时间混淆,典型例子是,电影中车轮倒转的现象。
(《数字图像处理》冈萨雷斯版,提供了详尽的例子,可以去参考)
平移、缩放、旋转
假设 $\mathscr F(f(x,y))=F(u,v)$,
平移 $\mathscr F(f(x-x_0,y-y_0)) = F(u,v) e^{-j2\pi (x_0u/M+y_0v/N)}$
- 幅度谱不变
- 相位谱变化
- (其中,M、N 是离散 FFT 的宽和高;若是连续 FFT,则其值为1)
缩放 $\mathscr F(f(ax, by)) = \dfrac{1}{|ab|}F(u/a, v/b)$
- 幅度谱相反比例缩放
- 相位谱同比例缩放
旋转
做极坐标变换:$x=r\cos \theta, y=r\sin\theta, u=w\cos \phi, v=w\sin \phi_0$
极坐标表示下,旋转为,$\mathscr F(f(r,\theta+\theta_0)) = F(w,\phi+\phi_0)$
- 幅度谱旋转
- 相位谱随着旋转
乘窗
假设窗口函数为 $w(x,y)$ (保留区域为1,其它为0),那么:
$g(x,y)= f(x,y) \cdot w(x,y)$
对应傅立叶变换为 $G(u, v) = F(u, v) \cdot W(u, v)$
裁剪 相当于 乘窗 + 平移
总结来说:
| 操作 | 幅度谱 | 相位谱 |
|---|---|---|
| 平移 | 不变 | 线性变化 |
| 缩放 | 相反比例缩放 | 同步缩放 |
| 旋转 | 随着旋转 | 随着旋转 |
周期性
对称性
实用案例
import numpy as np
sample_rate = 500 # 采样率为 500Hz
t_max = 5 # 时间为5秒
t = np.linspace(start=0, stop=t_max, num=sample_rate * t_max, endpoint=False) # 时间轴
# 创建信号:频率为 5 的信号 + 频率为 20 的信号
y = np.sin(2 * np.pi * 5 * t) + 0.8 * np.sin(2 * np.pi * 20 * t)
y_fft = np.fft.fft(y)
y_fft_magnitude = np.abs(y_fft)
画图展示 fft 和原始序列的关系
import matplotlib.pyplot as plt
fig = plt.figure(2)
axes = fig.subplots(nrows=2, ncols=1, sharex=True, sharey=False)
axes[0].plot(y)
axes[1].plot(y_fft_magnitude)
plt.show()
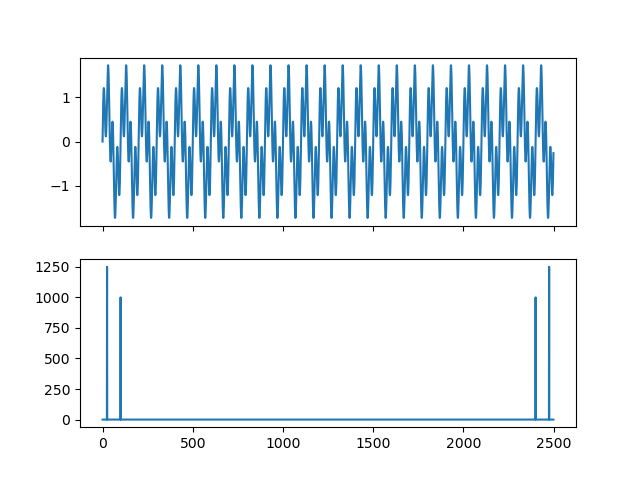
计算周期(完整代码)
# %%计算最强的周期
len_y = len(y)
# 频率轴
freq = np.fft.fftfreq(len_y, 1 / sample_rate)
# 找到最大幅度对应的频率,只取左半边
peak_frequency = freq[np.argmax(y_fft_magnitude[:len_y // 2])]
# 周期是频率的倒数
period = 1 / peak_frequency
# 打印结果
print(f"主要周期: {period}秒")
# %%找到所有的周期。
all_possible = np.argsort(y_fft_magnitude[:len_y // 2])[::-1]
pred_i = all_possible[0]
for i in all_possible:
# 如果强度比前一个小太多(这里是小一半),就停了
if y_fft_magnitude[i] < y_fft_magnitude[pred_i] / 2:
break
print(f"周期:{1 / freq[i]},对应强度 {y_fft_magnitude[i]}")
结果:
主要周期: 0.2秒
周期:0.2,对应强度 1250.0
周期:0.05,对应强度 999.9999999999999
注
- 如果
y的均值不为0,那么y_fft_magnitude[0]代表的是直流通量。它会比较大,导致上面的代码报错。解决方法有2种- 跳过
all_possible[0] - 用
y = y - y.mean()使其均值归零
- 跳过
离散傅立叶变换案例:周期、幅度谱、相位谱
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks
# %% 测试信号: 三个正弦波
fs = 1000 # 采样率
t_max = 5
t = np.linspace(0, t_max, int(fs * t_max), endpoint=False)
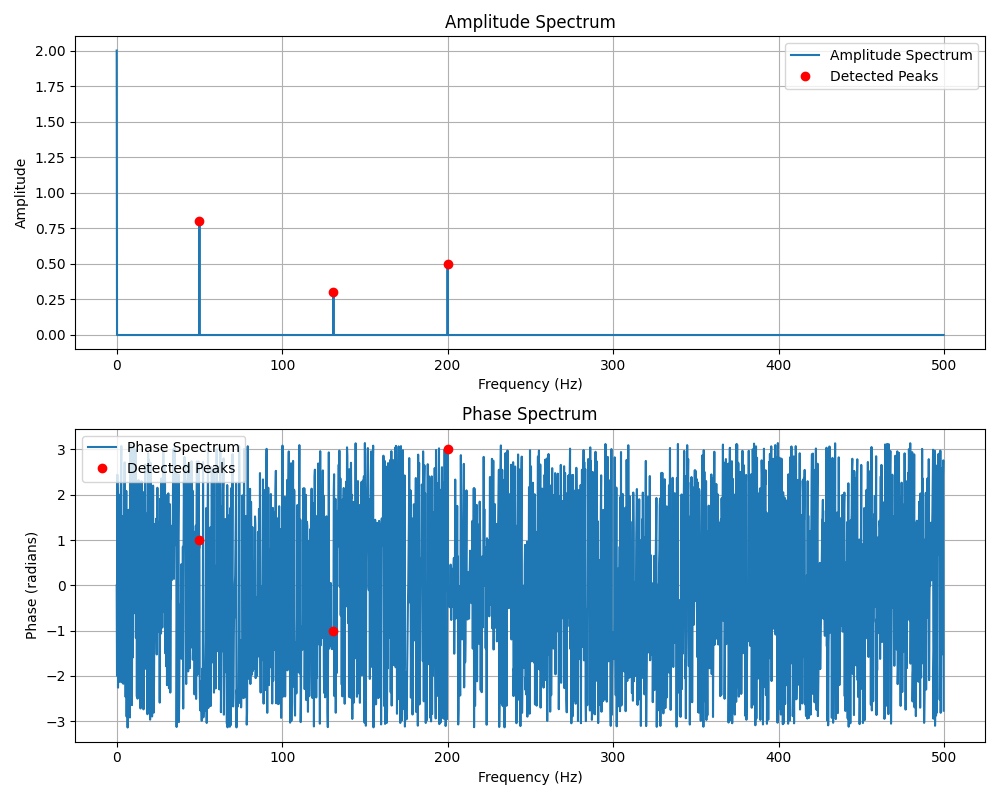
x = 2 \
+ 0.8 * np.cos(2 * np.pi * 50 * t + 1) \
+ 0.3 * np.cos(2 * np.pi * 131 * t - 1) \
+ 0.5 * np.cos(2 * np.pi * 200 * t + 3)
# %% 寻找频率
amp_threshold = 0.05
plot = True
N = len(x)
# FFT
X = np.fft.fft(x)
freqs = np.fft.fftfreq(N, d=1 / fs)
# 单边谱
pos_mask = freqs >= 0
freqs = freqs[pos_mask]
amps = np.abs(X[pos_mask]) / N * 2 # 单边幅度谱,归一化
# 修正
amps[0] /= 2
if N % 2 == 0:
amps[-1] /= 2
# 找峰值
peak_indices, _ = find_peaks(amps, height=amp_threshold)
freqs_found = freqs[peak_indices]
amps_found = amps[peak_indices]
# 频率谱
phase = np.angle(X[pos_mask])
phase_found = phase[peak_indices]
# 绘图
if plot:
plt.figure(figsize=(10, 8))
# 幅度谱
plt.subplot(2, 1, 1)
plt.plot(freqs, amps, label="Amplitude Spectrum")
plt.plot(freqs_found, amps_found, "ro", label="Detected Peaks")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.title("Amplitude Spectrum")
plt.grid(True)
plt.legend()
# 相位谱
phase = np.angle(X[pos_mask]) # 相位谱
plt.subplot(2, 1, 2)
plt.plot(freqs, phase, label="Phase Spectrum")
plt.plot(freqs_found, phase_found, "ro", label="Detected Peaks")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Phase (radians)")
plt.title("Phase Spectrum")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
if amps[0] > amp_threshold:
print(f"找到直流分量, 幅度: {amps[0]:.3f}")
print("找到的频率成分:")
for f, a in zip(freqs_found, amps_found):
# 找到对应频率的相位
idx = np.argmin(np.abs(freqs - f)) # 找到频率对应的索引
phi = phase[idx]
print(f"频率: {f:.2f} Hz, 幅度: {a:.3f}, 相位: {phi:.3f} rad")
输出:
找到直流分量, 幅度: 2.000
找到的频率成分:
频率: 50.00 Hz, 幅度: 0.800, 相位: 1.000 rad
频率: 131.00 Hz, 幅度: 0.300, 相位: -1.000 rad
频率: 200.00 Hz, 幅度: 0.500, 相位: 3.000 rad
问题与解释:
freqs 是频率数组,
- 值为 $[0, \Delta f, 2\Delta f, 3\Delta f, \dots, (N/2-1)\Delta f, -N/2\Delta f, \dots, -2\Delta f, -\Delta f]$
- 其中:$\Delta f = \dfrac{1}{N \cdot d} = \dfrac{f_s}{N}$,叫做频率分辨率
freqs[i]指的是 iHz,对应的幅度freqs[0]对应0Hz,是直流分量,其幅度应当做修正amps[0]/2- 当 N 为偶数时,最高频率点也要修正
amps[-1]/2
谱泄露 导致结果不准
x = 0 + 0.8 * np.sin(2 * np.pi * 5 * t) + 0.3 * np.sin(2 * np.pi * 12.5 * t)- 这是因为,`$\Delta f =1000/5000=0.2$,而频率 12.5 不能整除 0.2,意味着这个信号的频率无法对齐 FFT 的栅格点,从而会产生能量“ 泄露”到多个频率点里
- 也就是说,“主峰”无法落在 12.5Hz,而是分散到 12.4Hz 和 12.6Hz
- 解决方案:
- 方案1(很苛刻):减少
t_max,使t_max = 0.08 * k,这样 12.5Hz 正好能对齐 FFT 点 - 方案2:乘以一个窗函数,使最大峰位置恢复正确
- 方案3(其实也不是很准):用更准确的峰值估计方法(插值/拟合)。例如,选取
amps[k-1], amps[k], amps[k+1]三个点做抛物线插值。
- 方案1(很苛刻):减少
物理意义
- 假设 $x(t)$ 的傅立叶变换是 $X(k)$
- 那么写成复函数形式 $X(k)=\lvert X(k) \rvert e^{j \arg(X(k))}$
- 幅度谱 就是 $\lvert X(k)\rvert$
- 相位谱 就是 $\arg(X(k))$
它们的物理意义:
假设信号是多个正弦波的叠加: $x(t) = \sum_k A_k \cos( 2 \pi f_k t + \phi_k )$
FFT 完毕后:
- 幅度谱告诉你:在 $f_k$ 这个频率处,幅度是 $A_k$
- 相位谱告诉你:这个频率分量的初相 $\phi_k$ 是多少
举例来说,假设信号是 $x(t) = 1.0 \cdot \cos(2\pi \cdot 5 t + 30^\circ) + 0.5 \cdot \cos(2\pi \cdot 10 t - 60^\circ)$
FFT 后:
- 幅度谱:
5 Hz → 幅度 ~ 1.0 10 Hz → 幅度 ~ 0.5 - 相位谱:
5 Hz → 相位 ~ +30° (表示5 Hz分量的波峰比余弦滞后 30°) 10 Hz → 相位 ~ -60° (表示10 Hz分量的波峰比余弦超前 60°)
其它
- 在可视化时,人类习惯把零频率从数组开头搬到数组中心
- 把这样的频率:
0Hz +f1 +f2 ... +fmax -fmax+Δ ... -f1 - 变成这样的频率:
- fmax ... -f1 0Hz +f1 ... +fmax - 涉及到的函数:
np.fft.fftshift,np.fft.ifftshift(fshift)
- 把这样的频率:
二维离散傅立叶变换
照片、低通滤波、高通滤波,参考:https://www.guofei.site/2020/06/06/cv3.html
下面是对于二维fft的模拟
import numpy as np
import matplotlib.pyplot as plt
# %% 生成测试图像
M, N = 256, 256
x = np.arange(M)
y = np.arange(N)
X, Y = np.meshgrid(x, y, indexing='ij')
img = 128 \
+ 50 * np.cos(2 * np.pi * 4 * X / M + 0.5) \
+ 30 * np.cos(2 * np.pi * 8 * Y / N - 1.0) \
+ 20 * np.cos(2 * np.pi * 12 * (X + Y) / N + 0.8) # 一个45度的斜的周期样条
img = img.astype(float)
img = np.clip(img, 0, 255)
# %% 2D FFT
F = np.fft.fft2(img)
amps = np.abs(F) / N / M * 2
phase = np.angle(F)
# %% 修正
# 负的区域去掉
amps = amps[:M // 2 + 1, :N // 2 + 1]
phase = phase[:M // 2 + 1, :N // 2 + 1]
# DC补正
amps[0, 0] /= 2
# 偶数补正
if M % 2 == 0:
amps[-1, :] /= 2
if N % 2 == 0:
amps[:, -1] /= 2
# %%找峰值
amp_threshold = 2
mask = amps > amp_threshold
coords = np.where(mask)
for i in range(len(coords[0])):
u_idx, v_idx = coords[0][i], coords[1][i]
if u_idx == v_idx == 0:
print(f"找到直流分量, 幅度: {amps[u_idx, v_idx]:.3f}")
else:
print(f"周期 = {u_idx}, {v_idx}; 幅度:{amps[u_idx, v_idx]:0.3f}, 相位:{phase[u_idx, v_idx]:0.3f}")
# %% 绘图
plt.figure(figsize=(12, 5))
plt.subplot(1, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('Original image')
plt.axis('off')
plt.subplot(1, 3, 2)
plt.imshow(np.log1p(amps), cmap='gray')
plt.scatter(coords[0], coords[1], c='r', marker='o')
plt.title('amps (log)')
plt.axis('off')
plt.subplot(1, 3, 3)
plt.imshow(phase, cmap='gray')
plt.scatter(coords[0], coords[1], c='r', marker='o')
plt.title('Phase Spectrum')
plt.axis('off')
plt.tight_layout()
plt.show()
找到直流分量, 幅度: 128.000
周期 = 0, 8; 幅度:30.000, 相位:-1.000
周期 = 4, 0; 幅度:50.000, 相位:0.500
周期 = 12, 12; 幅度:20.000, 相位:0.800

参考文献
张筑生:数学分析新讲
李红:《复变函数与积分变换》高等教育出版社
“十五”国家规划教材《复变函数与积分变换》高等教育出版社
钟玉泉:《复变函数论》高等教育出版社
冈萨雷斯:《数字图像处理》
您的支持将鼓励我继续创作!
