【数据结构1】线性表

主要内容

顺序表
链表
- 单链表
- 单循环链表
- 双向循环链表
跳跃表
并查集

1. 顺序表

顺序表是在内存中连续存放的数组。
顺序表有如下操作：

初始化
求元素个数
在i位置插入一个元素。从后往前，依次后移1格，直到i位置。
删除一个元素。类似的相反操作

因此，顺序表的增、删操作，时间复杂度都是 O(n)

2. 单链表

有两种：带头结点单链表（用一个空节点作为头部结点），不带头结点单链表（用第一个数据节点作为头部结点）
不带头结点单链表对第一个元素增、删时，与其它元素的增删操作不一致，所以一般使用带头结点

带头节点的单链表

class Node(object):
    def __init__(self, val=None, next=None):
        self.val = val
        self.next = next

    def __repr__(self):
        return str(self.val)


# 带dummy的LinkedList
class MyLinkedList:
    def __init__(self):
        self.head = Node(val='□')  # 打印要用
        self.size = 0

    def get(self, index):
        assert 0 <= index < self.size
        curr = self.head
        for _ in range(index + 1):
            curr = curr.next
        return curr.val

    def add_at_tail(self, val):
        curr = self.head
        while curr.next:
            curr = curr.next
        curr.next = Node(val)
        self.size += 1

    def add_at_index(self, index, val):
        assert 0 <= index < self.size
        curr = self.head
        for i in range(index):
            curr = curr.next
        curr.next = Node(val=val, next=curr.next)
        self.size += 1

    def delete_at_index(self, index):
        assert 0 <= index < self.size
        curr = self.head
        for i in range(index):
            curr = curr.next
        curr.next = curr.next.next

        self.size -= 1

    def from_list(self, lst):
        curr = self.head
        for val in lst:
            curr.next = Node(val=val)
            curr = curr.next
            self.size += 1

    def to_list(self):
        curr = self.head.next
        res = list()
        while curr is not None:
            res.append(curr.val)
            curr = curr.next
        return res

    def __repr__(self):
        return ' -> '.join([self.head.val] + [str(i) for i in self.to_list()])


if __name__ == "__main__":
    my_linked_list = MyLinkedList()
    lst = [1, 1, 2, 3, 4, 5]
    my_linked_list.from_list(lst)
    assert my_linked_list.to_list() == lst
    print(my_linked_list)

刷题技巧

使用带dummy的链表，往往可以使代码更好写。LeetCode 给的格式都是不带头节点的，做个 next 即可
遇到多链表的时候，你可能需要 curr = curr.next if curr else curr，这样 curr 如果为 None，就表示它早已到达终点

Two Pointer Technique

Two pointers starts at different position: one starts at the beginning while another starts at the end;
Two pointers are moved at different speed: one is faster while another one might be slower.

一个来自 LeetCode的案例 141. Linked List Cycle

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if head is None:
            return False
        fast=head
        slow=head
        while True:
            if (fast is None) or (slow is None):
                return False
            if (fast.next is None) or (fast.next.next is None) or (slow.next is None):
                return False
            fast=fast.next.next
            slow=slow.next
            if fast is slow:
                return True

reverse 链表

def reverseList(self, head):
    if head is None:
        return None
    curr=head
    while curr.next:
        tmp=curr.next
        curr.next=curr.next.next
        tmp.next=head
        head=tmp
    return head

环形链表

其实现与单链表很相似，不过检查结束的条件是 curr.next == head

双向链表

跳跃表

参考

为什么：

顺序表。查找如果可以用二分法，复杂度是 O(logn), 插入和删除都是 O(n)
链表不能用二分法，查找复杂度是O(n),插入、删除复杂度是 O(1)
二叉树，虽然插入、删除、查找也是 O(logn)，但仅限于平衡二叉树，遇到严重偏到一边的二叉树，复杂度仍然是 O(n)
红黑树。本身实现很复杂，并且插入、删除时，同时做一次平衡，提高了一定的花销。

跳跃表是什么？

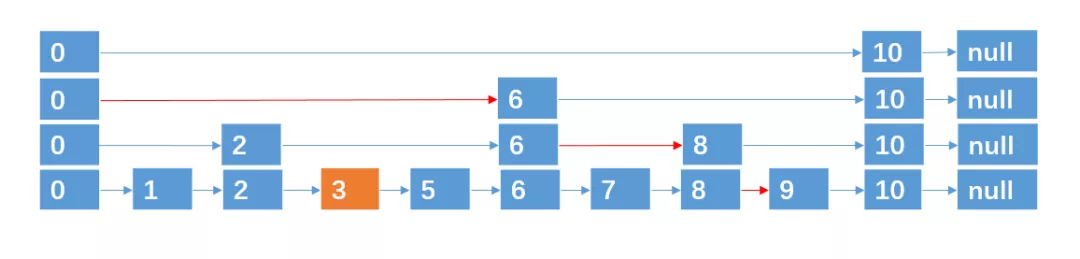
catenary1

查找：这就可以用二分法了，复杂度 O(logn)
插入：抛硬币来决定新插入结点跨越的层数：每次我们要插入一个结点的时候，就来抛硬币，如果抛出来的是正面，则继续抛，直到出现负面为止，统计这个过程中出现正面的次数，这个次数作为结点跨越的层数。
删除：从每个链条删除即可

查找、插入、删除复杂度都是 O(logn)

总结下跳跃表的有关性质：

跳跃表的每一层都是一条有序的链表.
跳跃表的查找次数近似于层数，时间复杂度为O(logn)，插入、删除也为 O(logn)。
最底层的链表包含所有元素。
跳跃表是一种随机化的数据结构(通过抛硬币来决定层数)。
跳跃表的空间复杂度为 O(n)。

矩阵

压缩存储：

上/下三角矩阵，用线性表存一半，k和(i,j)的互相计算
稀疏矩阵：[[i,j,val],[...],...] 可以使用链表来存
- 转置非常方便

栈和队列

主要内容：

Stack
Queue：一种 first-in-first-out (FIFO) 算法
优先队列、优先堆：Last-in-first-out Data Structure（先进先出表）
多级反馈队列

栈和队列实际上是（前面介绍的）线性表的应用

我们知道，list天然地适合做 Stack，即尾部入，尾部出
我们又知道 list 删除头部的元素是极为低效的，解决方法是很简单，只要增加一个指向头部的指针即可。

栈

用 list 实现栈

class Stack(list):
    def push(self, term):
        self.append(term)

    def take(self):
        return self.pop()

队列：C

用C实现：

链表
两个 stack 可以构造一个 queue：https://leetcode.cn/problems/implement-stack-using-queues/
循环array可以构造一个 queue：https://github.com/guofei9987/c-algorithm/tree/master/DynamicArray

队列的其它实现

Queue：借用 deque（底层是循环 array），是效率最高的了
Queue1：用 list 实现队列
Queue2：用 list 实现队列，并且每次take都清除多余
Queue3：用链表
Queue4：用 list 实现队列，并且当多余信息过多时清除多余
Queue5: 用两个 stack 可以模拟一个 queue，效率仅比 deque 慢一点点

# 缺点：内存会一直增加
class Queue1(list):
    def __init__(self):
        super(Queue1, self).__init__()
        self.head_idx = -1

    def push(self, term):
        self.append(term)

    def take(self):
        self.head_idx += 1
        return self[self.head_idx]


# 缺点：虽然内存控制住了，但是 take 操作耗时加倍
class Queue2(object):
    def __init__(self):
        self.q = list()

    def push(self, term):
        self.q.append(term)

    def take(self):
        self.q = self.q[1:]


# 用链表做，效率和 2 一样
class Node(object):
    def __init__(self, val):
        self.val = val
        self.next = None


class Queue3(object):
    def __init__(self):
        self.head = Node(None)
        self.tail = self.head

    def push(self, term):
        node_new = Node(term)
        self.tail.next = node_new
        self.tail = node_new

    def take(self):
        res = self.head.next
        self.head.next = res.next
        return res


# 当已经出列的元素多余100个时，重整list，这应该是比较均衡的方案了
class Queue4(object):
    def __init__(self):
        self.q = list()
        self.head_idx = -1

    def push(self, term):
        self.q.append(term)

    def take(self):
        # 这里还可以根据列表大小和实际功能，做动态更改，而不是固定100
        if self.head_idx == 100:
            self.q = self.q[101:]
            self.head_idx = -1
        self.head_idx += 1
        return self.q[self.head_idx]


from collections import deque

# 双 stack 可以实现一个 queue
class Queue5:
    def __init__(self):
        self.stack1 = list()
        self.stack2 = list()

    def push(self, val):
        self.stack1.append(val)

    def take(self):
        if not self.stack2:
            self.stack2 = self.stack1[::-1]
            self.stack1 = list()
        return self.stack2.pop()


# 使用 deque （循环array），最快的方案
class Queue(object):
    def __init__(self):
        self.q = deque()

    def push(self, term):
        self.q.append(term)

    def take(self):
        return self.q.popleft()

性能测试：

import datetime

Classes = [Queue1, Queue2, Queue3, Queue4, Queue5, Queue]


def test_time(q_class):
    num = 100
    start_time = datetime.datetime.now()
    for i in range(num):
        queue = q_class()

        for i in range(10000):
            queue.push(i)

        for i in range(10000):
            queue.take()

    print(datetime.datetime.now() - start_time)


for q_class in Classes:
    test_time(q_class)

00:00.327828
00:11.765587
00:00.814363
00:00.459293
00:00.262654
00:00.238956

Circular Queue

用list来模拟Cirular Queue

num_list[i%len_list]

优先队列

这样的队列：每个项目对应一个优先度，出列顺序按照优先度来排。

常用于计算机进程分配、医院急救队列
一般用二叉堆来实现，二叉堆见于另一篇文章。

应用

案例1：queue的一种典型应用场景是Breadth-first Search (BFS)

queue 案例2
题目灵感来自LeetCode题目,我给出的解答见于这里

例子：

input_queue=[1,2,3,4,5]    
stack=[2,1]
pointer=0
for i in input_queue:
    stack.append(i)
    # 后两行是先出的功能：
    stack_out=stack[pointer]
    pointer+=1

# 事实上，因为可以使用stack[-1],stack[-2]这些命令，所以 pointer 这个变量往往不必定义
# 会有内存浪费，定期清理即可，参考代码： stack=stack[pointer:]

案例3：深度优先搜索 Depth-First Search (DFS)

案例4：200. Number of Islands