🔥【密码学】知识体系
🗓 2023年06月01日 📁 文章归类: 0x58_密码学
版权声明:本文作者是郭飞。转载随意,标明原文链接即可。
原文链接:https://www.guofei.site/2023/06/01/cipher.html
相关书目: 《深入浅出密码学》
一些概念
密码学要解决的问题
- 保密性 Confidentiality
- 完整性 Integrity
- 可用性 Availability
历史上的密码学
- 羊皮传书
- 藏头诗(实际上是一种隐写术)
- Caesar
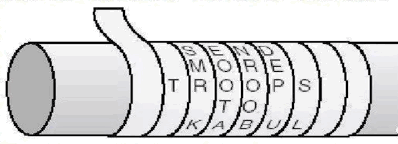
密码系统的组成
- 明文 Plaintext
- 密文 Ciphertext
- 密钥 key
- 加密算法 encipher
- 解密算法 decipher
分类1:根据明文变成密文的变换方法分类
| 类型 | 核心思想 | 示例 |
|---|---|---|
| 替换密码 Substitution Cipher | 用其他符号替代明文中的符号,顺序不变 | Caesar |
| 置换密码 Transposition Cipher | 保留原符号,但重新排列顺序 | Rail Fence |
| 乘积密码 Product Cipher | 结合替代与置换,以增强安全性 | DES、AES(现代密码多属此类) |
分类2:根据 key 数量
| 类型 | 特点 | 常见算法 |
|---|---|---|
| 对称密码 Symmetric Cryptography | 加密与解密使用同一把密钥(Same Key for Encryption and Decryption) | AES、DES、SM4 |
| 非对称密码 Asymmetric Cryptography | 加密与解密使用不同的密钥对(Different Keys: Public & Private) | RSA、DSA、ECC、NTRU、Rainbow |
- 对称密码
- 对称密码的一些说明
- 密码学假定信道本身不安全,而密钥应当双方都知道
- 因此通信之前双方需要在某个安全通道传输密码 key
- 非对称密码
- RSA:基于整数分解
- DSA:基于离散对数问题
- ECC:基于椭圆曲线
- NTRU:基于格理论,抗量子
- Rainbow:基于多变量多项式,用于数字签名
分类3:根据明文处理方式,对称密码还分为:
| 分类 | 加密单元 | 应用场景 |
|---|---|---|
| 分组密码 Block Cipher | 每次处理一组固定长度的数据块(Encrypt Data in Blocks) | 主要是民用/商用 文件加密、HTTPS DES(已不安全)、AES(目前广泛使用) |
| 流密码 Stream Cipher | 按比特/字节连续处理(Encrypt Data as a Stream) | 主要是军用 实时通信、无线传输 |
对称密码的一些说明
- 密码学假定信道本身不安全,而对称密码的密钥应当双方都知道
- 因此通信之前双方需要在某个安全通道传输密码 key
非对称密码的一些说明
- RSA:基于整数分解
- DSA:基于离散对数问题
- ECC:基于椭圆曲线
- NTRU:基于格理论,抗量子
- Rainbow:基于多变量多项式,用于数字签名
密码编码学(Cryptography):研究如何做密码编码
密码分析学(Cryptanalysis),是破解密码的研究,是对密码攻击
- 所用的方法:
- 经典密码分析(Classical Cryptanalysis)
- 数学分析法:发现加密方法内部结构的分析攻击
- 暴力破解:测试所有可能的密钥进行破解
- 实施攻击(Implementation Attack)
- 从旁道分析,如:测量处理私钥的处理器的功耗、电磁辐射、算法运行时的行为。前提是攻击者可以物理访问密码体制。
- 社会工程攻击。行贿、勒索、跟踪或侦探
- 经典密码分析(Classical Cryptanalysis)
- 密码分析面临的情况
- 仅知密文攻击(Ciphertext - only attack)。仅能获取到一些密文,尝试推导出明文或者密钥
- 已知明文攻击(Known - Plaintext attack)。除了拥有一定数量的密文外,还知道与之对应的明文。
- 选择明文攻击(Chosen - Plaintext attack)。可以任意选择明文,并获取对应的密文
- 密文攻击(Chosen - Ciphertext attack)。攻击者可以选择特定的密文,并获取这些密文对应的明文
- 密码学(Cryptology):就是密码编码学+密码分析学。
Kerckhoffs 原则:一个密码系统安全,不依赖算法的保密性,只依赖密钥的保密性。
- 否则一旦算法泄漏(很容易),整个密码系统就完蛋
- 公开算法,使得其受到广泛审查。假定某个人找到了密码系统的漏洞,对其最有利的做法是发论文,否则会被别人抢先。
- 公开算法,使公众可以信任它,而不是依赖测试机构的权威
- 密钥易于更换,算法不易更换
密码协议:利用密码学实现安全通信的一系列规则和步骤。例如 SSL、SSH、OAuth
密码安全
- 无条件安全:在攻击者拥有无限算力的情况下,一个密码体制也是安全的,叫做 无条件安全。密码学基本不研究这个。
- 计算安全:为了破解一个密码体制,最好的已知算法至少需要 t 个操作,叫做计算安全
- 破解所需时间超过信息本身的有效期,或者破解的成本高于信息本身的价值
- 存在问题:如 RSA 基于大整数因式分解,尽管因式分解算法是已知的,但我们不知道是否存在更好的因式分解算法。
数学基础
mod 与整数环
这个的系统组成一个环:
- $Z={0,1,2,…,m-1}$
- 定义两个运算符 $+, \cdot$
- $a+b\equiv c \mod m$
- $a\cdot b \equiv d \mod m$
性质
- 未必存在逆元(逆元定义为 $a\cdot a^{-1} \equiv 1 \mod m$)
- 当且仅当 $\gcd(a,m)=1$ 才存在逆元
替换密码
移位密码
凯撒密码(移位密码) 是一种最简单的替换密码,它把字母表向后移动 k 位,末尾放开头
- 算法(环的语言):
- 加密:$y\equiv x + k \mod 26$
- 解密:$x\equiv y - k \mod 26$
- 移位密码的评价:
- 移位密码的密钥只有 25 种,因此非常不安全。
- 它是替换密码的一种,可以使用字母频率分析法攻击它
仿射密码,在移位密码的基础上做一些改变
- 算法:
- 加密:$y \equiv a \cdot x + b \mod 26$
- 解密:$x \equiv a^{-1} \cdot (y - b) \mod 26$
- 密钥:$k = (a, b)$ ,其中 $gcd(a, 26)=1$
- 仿射密码的评价:
- a 可能取值为 1,3,5,7,9,11,15,17,19,21,23,25
- b 可能取值为 26 个
- 因此密钥空间为 12x26 = 312 ,也是非常不安全
单字母表密码 算法:
- 维护一个字母对字母的一一映射表(这个表就是密钥)
- 按照密钥做映射即可
攻击:
- 表面上上不同的组合有 $26!$ 种,需要暴力遍历几百年
- 实际上有一些高效的攻击手段
- 字母的频率是稳定的。在密文中也如此,统计密文中的字母频率可以大致推断是什么字母
- 类似的,连续密文也是可以统计,例如英语中,U总是跟着Q
- 如果发现了空格,可以找到高频短单词,例如 THE、AND
Playfair
单字母加密很容易被频率分析破解
- 多对一:分组,一次加密一组。Playfair密码
- 例如,构造的映射表是:8字母到8字母的映射
- 攻击者的词表就是 $26^8$ 大小
- 字母频率也不明显了
- 一对多(维吉尼亚密码)。明文中一个字母,可能映射为多个字母
Playfair cipher 用2个字母映射2个字母,
- 19世纪发明的,最初为了配合电报机使用。
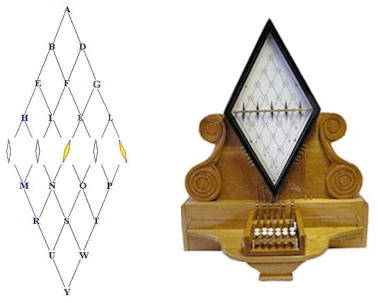
Playfair cipher 的算法:
- 密钥
- 共25个字母(规定ij不做区分)
- 按照惯例,密钥通常是规定某本书某一页某一位置
- 从这一位置起,开始提取字母(丢弃重复的),得到一个长度为 25 的字母排序。
- 这25个字母,可以写成一个 5x5 的矩阵,这就是密钥
- 分组。每两个分一组。
- 如果某组的两个一样,则填充最后一个为
X - 如果为奇数个,则最后一位填充(padding)
X,(现代密码的常见方法) - 举例。Plaintext 是
ballons,分组为ba lx on sx
- 如果某组的两个一样,则填充最后一个为
- 加密规则(以下面的密码表为例)
- 如果双字母在同一行,则用右边的字母代替。
AR -> RM - 如果双字母在同一列,则用下面的字母代替。
MU -> CM - 如果双字母不在同一行也不在同一列,则用对角上的字母代替。
HS -> BP,EA -> IM
- 如果双字母在同一行,则用右边的字母代替。

Playfair 同样可被攻击
- 词表共 $26\times 26 = 676$ 个元素,用现代计算机,只要截获几百个单词就可以很快破解
- 改进:提高分组大小,例如 8个一组,词表就是 $26^8$ 大小
维吉尼亚密码 的思路是使映射关系不唯一。例如,一个字母有时候按照词表1映射,有时候按照词表2映射。
一个典型做法:
- 每个词表都是凯撒密码,
- 假设密码
KEY = DECEPTIVE,第一个字母按照k='D'的凯撒密码加密,第二个字母按照k='E'的凯撒密码加密
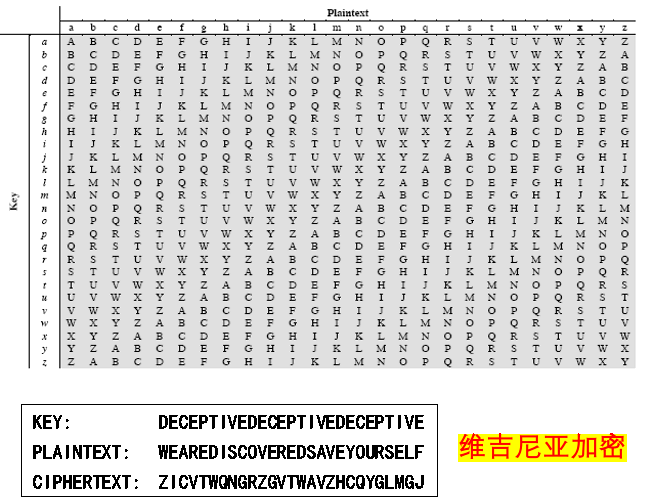
攻击方法
- 注意到维吉尼亚加密法,其
k是有周期的 - 一旦知道key的长度,就很容易用字频分析
- 如何找到 key 的长度呢?在密文中找周期,周期的公约数可能就是 key 的长度(多试几次)

(这个例子是故意造了个容易找周期的情况)
改进思路:
- key 不再使用周期性的循环使用,而是使用已解出的明文作为新的密码
- 这就是 Autokey Cipher

攻击方法
- Plaintext 本身也用作 key,可惜它们都是有频率分布的
- 例如,字母
E在 Plaintext 出现概率很高,因此在 key 中的出现概率也很高,因此E加密E的概率也很高 - 因此也可以用频率统计来攻击
综上,我们如何找一个合适的密码系统呢?核心思路就是如何屏蔽掉统计规律。
Vernam 加密
特点:
- 加密函数和解密函数是同一个函数
- 计算性能高,只需要一个 XOR 操作
- 密码序列是一串随机数,由随机数生成器生成,但是比普通的随机数生成器要求不可预测(也就是根据已生成的随机数,不能预测未来的随机数)。
Vernam 加密(Vernam Cipher)基本单位是位(bit)。其算法是明文与密文逐位 XOR 运算
- $x_i, y_i, s_i \in { 0, 1 }$
- 加密:$y_i = x_i \oplus s_i$
- 解密:$x_i = y_i \oplus s_i$
- 特点:硬件/软件实现高效,适用于实时通信;安全性取决于密钥流的不可预测性。
- 1918年 Vernam 提出并申请专利
- 1949年 香农证明了 OTP 就是 无条件安全的(无条件安全的密码体制很难设计)
- OTP在下面介绍
- OTP 的缺点是密钥分发极为困难
一次一密(OTP,One-Time Pad) 是 Vernam 密码的一个特例:
- 密钥 长度 = 明文长度;
- 密钥 真随机;
- 密钥 只使用一次,之后立即废弃;
- 密钥 保密且双方共享。
据传言,在冷战期间白宫和克里姆林宫之间的红色电话就是使用 OTP 加密的。但没有大规模使用,它有缺陷:
- 真随机数设备有成本
- Alice 必须把 ${ s_i }$ 安全的传递到 Bob,比如写入到 CD,让一位特工做信使
- ${ s_i }$ 用完后,还需要再次传递
基于移位寄存器的序列密码
接上文 OTP,想到用伪随机数生成器代替真随机数生成器,来生成 ${ s_i }$,这样密钥就是 seed,但这个想法是 不可行的,解释如下:
- 随机数生成器基于线性同余发生器:$S_0 = seed, S_{i+1}\equiv A S_i + B \mod m$
- 加密方式同 OTP
- 加密:$y_i = x_i \oplus s_i$
- 解密:$x_i = y_i \oplus s_i$
为什么这个方案是不可行的呢?
- 如果攻击者 Oscar 猜出部分明文(比如文件头信息更容易猜),那么立即结合密文可以计算出 ${ s_i }$
- 然后解方程 $S_2 \equiv A S_1 + B \mod m; S_3 \equiv A S_2 + B \mod m$,即可得到 $A,B$
- 根据 $\gcd(S_1-S_2,m)$ 取值,可以有多解或唯一解。然后根据其它分片可以唯一得到密钥
实际上相当多的伪随机数生成器都不是密码学安全的,我们需要专门设计伪随机数生成器:例如 线性移位寄存器(LFSR)
- 许多序列密钥是利用 LFSR 来实现的,例如 A5/1
- 构建方法很多,这里只介绍一种
LFSR 是用一个电路实现的,这个电路中有 m 个触发器,
例如,m =3 的情况下,LFSR 用数学描述是:
- 初始化 $s_0,s_1,s_2$
- $s_{i+3} \equiv s_{i+1} + s_i \mod 2$
性质:
- 当然,它是一个周期序列
- 它的周期是多少取决于 m 和初始化的值。一个 m 位的 LFSR,有 $2^m-1$ 种非零状态,因此它最大可能的周期为 $2^m-1$
如何攻击?
- 只要 Oscar 知道度为 m 的 LFSR 的 2m 个输出位,就可以列方程来解出参数
- 可以得到 m 个线性等式进而用高斯消元法来计算参数
- 然而,它并没有丧失所有密码属性。有不少序列密码都是使用多个LFSR 的组合构建强壮的密码体制。
Trivium 是一个较新的序列密码,它的密钥长度为 80 位。Trivium 基于三个移位寄存器的组合。然后在得到每个寄存器的输出时使用了非线性组件。
总体来说,许多序列密码的安全性都是未知的,而且很多已经被破解了。
置换密码
字母不变,打乱其顺序
简单的置换密码
Rail Fence密码 先横向写,然后纵向取,得到密文。
例如,一个深度为 k 的 Rail Fence,如下(代码比文字更容易说明)
plaintext = 'meetmeafterthetogapartyat8pm'
ciphertext = ''
k = 5
# (还需要padding,使其长度为 k 的整数倍)
for i in range(k):
ciphertext += plaintext[i::k]
前面提到的羊皮传书就是一种 Rail Fence 密码
行置换密码
在 Rail Fence 的基础上添加一个规则:
纵向取的时候,按照 Key 规定的顺序取。

转子机:古典密码的最高峰
二战期间广泛使用,是一种乘积密码
Enigma 机为例


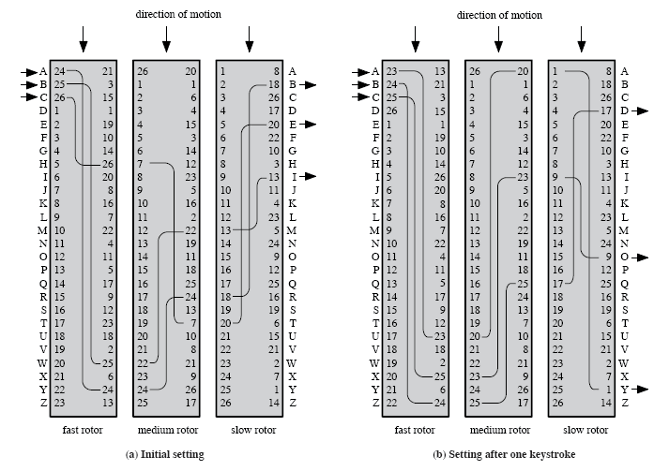
分组密码
强加密算法一般基于两种本原操作
- 混淆(Confusion):使密钥和密文尽可能模糊
- 扩散(Diffusion):一个明文符号影响多个密文符号
DES
- 对称密码
- 迭代算法,每个分组加密16轮
AES
- 分组长度 128,密钥长度 128/192/256
- 设计简单、代码紧凑、运行速度快
- 可以在8位CPU上运行,需要4k存储空间
流密码
RC4、ChaCha20 等
非对称密码
对称密码的缺点
- 密钥分发:需要一个安全渠道分发密钥
- 没有不可否认性:只要知道密钥,就可以加密和解密
- 用户增多时,密钥数量膨胀。n个用户互相通信,需要两两密钥,就是 n(n-1)/2 个密钥。非对称密码需要 2n 个密钥(每人公私各1个)
- 非对称密码也有其缺点,就是速度较慢。一个用法是,用非对称密码来交换“对称密码的密钥”,然后用对称密码相互通信。
非对称密码的使用(A 发送给 B)
- Bob 的公钥是公开的(例如放在主页或公告板)
- Bob 的私钥是保密的,只有自己知道
- Alice 使用 Bob 的公钥加密,然后把密文传递给 Bob
- Bob 用自己的私钥解密,得到明文
公开密钥系统的 6个要素
- 明文 Plaintext
- 公开密钥(PK, Public Key)
- 私有密钥(SK, Secret Key)
- 加密算法 encipher
- 密文 Ciphertext
- 解密算法 decipher
公开密钥算法的基本要求(A 发送给 B)
- B 容易通过计算产生一对密钥($PK_b$,$SK_b$)
- A 容易计算产生密文,$C = E_{PK_b}(M)$
- B 容易计算解密,得到解密后的明文,$M = D_{SK_b}(C) = D_{SK_b}(E_{PK_b}(M))$
- 敌对方即使知道 PK,要确定 SK,计算上不可行
- 敌对方即使知道 PK 和 Ciphertext,要确定 Plaintext,计算上不可行
- 密钥对相互可以交换使用 $M = D_{SK_b}(E_{PK_b}(M)) = D_{PK_b}(E_{SK_b}(M))$
- 也就是说:用公钥加密的,可以用私钥解密;用私钥加密的,可以用公钥解密
- 前者可以用来做 加密通信,后者可以用来做 数字签名
- 上面提到的 容易计算、计算上不可行 是有严格定义的,是根据计算复杂度定义的。
签名的需求
- 身份的认证
- 抗抵赖
数字签名 (B 发送给 A)
- 过程
- B 用自己的私钥加密,然后发送给 A
- A 用 B 的公钥解密(验证签名的过程)
- 身份认证 A 用 B 得公钥把信息解密了,说明发送方只可能是 B
- 抗抵赖 A 可以用密文 + B 的公钥,找第三方裁决,很容易确定密文来自 B
- 对称密码系统无法解决这两个需求,因为 A 和 B 知道的信息一样多。
综上,非对称密码系统的使用场景:
- 加密通信。(对称密码也有这个功能)
- 交换密钥
- 数字签名
- 身份认证
- 抗抵赖
| RSA | Diffie-Hellman | DSA | |
|---|---|---|---|
| 保密通信 | ✅ | ❌ | ❌ |
| 密钥交换 | ✅ | ✅ | ❌ |
| 数字签名 | ✅ | ❌ | ✅ |
RSA
- 1977年Rivest, Shamir和Adleman提出
- 是一种分组加密算法
- 基于数论的论断:两个大素数相乘很容易,但是分解计算上不可能
RSA 密钥生成算法
- 生成两个大素数 $p$, $q$
- 100位(十进制)以上
- 有一些算法,复杂度是概率多项式。常见的:
- Solovay-Strassen 素性测试
- Miller-Rabin 素性测试
- 计算 $n = p \times q$
- 计算 $\phi(n) = (p-1)(q-1)$
- 这是小于 n 并且与 n 互素的整数个数
- 随机选择一个数 $e$,使其满足 $1<e<\phi(n)$,并且 $\gcd (e,\phi)=1$ (也就是互素)
- 算法复杂度为多项式。
- 算法:找一个素数 e,并且它与 $\phi(n)$ 互素
- 解方程 $e\times d \equiv 1(\mod \phi(n))$,求出 d
- 辗转相除法(欧几里得算法)
- 保密 $d$, 销毁 $p,q$,公开 $n,e$
- 公钥 PK = $(e,n)$
- 私钥 SK = $(d,n)$
RSA加密算法 RSA 的加密和解密过程
- 公钥为 (e, n),私钥为 (d, n)
- 假设明文为数字 m
- 公钥加密 $c = (m^e) \mod n$ (必须满足 $m<n$,否则的话要对 m 进行分组)
- 私钥解密 $m = (c^d) \mod n$
- 发现加密算法和解密算法完全一样,因此可以用同一套硬件。(所以 RSA 是一个优秀的算法)
- 两个运算正好是逆运算,这个可以证明
- p, q 要足够大,否则容易通过公开的 n 计算出来
- 模指数运算 ($m = (c^d) \mod n$) 是有算法优化的(下面)
- 必须满足 $m<n$,否则的话要对 m 进行分组
- 公钥解密 $m = (c^e) \mod n$
- 私钥加密 $c = (m^D) \mod n$
# RSA key generation — toy example (DO NOT use in production)
# p, q are small primes just for demonstration
from math import gcd
def egcd(a, b):
"""扩展欧几里得算法,返回 (g, x, y) 使得 ax + by = g = gcd(a,b)"""
if b == 0:
return (a, 1, 0)
g, x1, y1 = egcd(b, a % b)
return (g, y1, x1 - (a // b) * y1)
def modinv(a, m):
"""模逆:返回 a 在模 m 下的乘法逆元(若存在)"""
g, x, _ = egcd(a, m)
if g != 1:
raise ValueError("inverse does not exist")
return x % m
# 1) 选两个素数(示例用小素数)
p, q = 61, 53
# 2) 计算 n 和 φ(n)
n = p * q
phi = (p - 1) * (q - 1)
# 3) 选择 e,满足 1 < e < φ(n) 且 gcd(e, φ(n)) = 1
# 经典选择是 65537;这里为了示例取更小的 17
e = 17
assert 1 < e < phi and gcd(e, phi) == 1
# 4) 计算 d,使 e*d ≡ 1 (mod φ(n))
d = modinv(e, phi)
print("Public Key (PK) =", (e, n))
print("Private Key (SK) =", (d, n))
# 5) 演示加解密(m 必须小于 n)
def encrypt(m, e, n):
"""RSA 加密:c = m^e mod n"""
return pow(m, e, n)
def decrypt(c, d, n):
"""RSA 解密:m = c^d mod n"""
return pow(c, d, n)
m = 42
c = encrypt(m, e, n)
m_dec = decrypt(c, d, n)
print("\nPlaintext m =", m)
print("Ciphertext c =", c)
print("Decrypted m =", m_dec)
返回:
Public Key (PK) = (17, 3233)
Private Key (SK) = (2753, 3233)
Plaintext m = 42
Ciphertext c = 2557
Decrypted m = 42
关于 模指数运算 的优化:
- 假设要计算 $11^{23} \mod 187$
- 先得到 $11^{23} \mod 187 = [(11^{1} \mod 187) * (11^{2} \mod 187) * (11^{4} \mod 187) * (11^{8} \mod 187) * (11^{8} \mod 187) * ] \mod 187$
- 然后递归计算:
- $11^{1} \mod 187 = 11$
- $11^{2} \mod 187 = (11*11) \mod 187 = 121$
- $11^{4} \mod 187 = (121*121) \mod 187 = 55$
- $11^{8} \mod 187 = (55*55) \mod 187 = 33$
RSA算法的评价
- 取决于模n分解的困难性,目前最快的算法复杂性为 $O(\exp(\sqrt{\ln(n)\ln\ln n}))$
- 但是并没有证明分解大整数是 NP 问题。
- 也没哟证明对 RSA 的攻击难度与分解大整数等价
- 目前,RSA 的一些变种算法已被证明等价于大数分解
- 由于有很多大数运算,因此性能较慢,一般只用于少量数据加密
- RSA 被研究的最为广泛,普遍认为是目前最优秀的公钥方案之一
非对称密码的理论基础
- 单向函数
- 一个函数 $f(x)$,对于任意 $x$,$f(x)$ 容易计算,同时对于几乎所有 $y$,$f^{-1}(y)$ 计算上不可行,那么 $f(x)$ 叫做单向函数
可以提供单向函数的数学难题:
- 大整数分解问题(IFP)
- 离散对数问题(DLP)
- 椭圆曲线离散对数问题(ECDLP)
- 等等
- 单向陷门函数
- 一个 单向函数,如果 $f^{-1}(y)$ 在已知某些辅助信息的情况下,容易求解,那么称为单向陷门函数
构造公钥密码系统的关键就是构造合理的单向陷门函数
Diffie-Hellman
介绍
- 第一个公钥方案
- 应用广泛(如 SSH)
- 用于 安全密钥交换
- 不能直接用做大量数据传输
- 不直接加密消息,而是双方协商出一个共享密钥
- 允许两个用户安全建立秘密信息,用于后续通讯
- 算法安全性依赖于 有限域上计算离散对数的问题
算法-密钥生成
- 通信双方/多方选择一个大素数 $p$,以及 $p$ 的一个原根
- 用户 A 随机选择一个数 $X_a<p$,然后计算 $Y_a = a^{X_a} \mod p$
- $X_a$ 是私钥,$Y_a$ 是公钥
- 用户 B 随机选择一个数 $X_b<p$,然后计算 $Y_b = a^{X_b} \mod p$
- $X_b$ 是私钥,$Y_b$ 是公钥
算法-使用
- 一方传输 $p$ 和 $a$
- 双方要传输的是某个对称密码系统的密钥 $K = a^{X_a X_b} \mod p$
- A 通过计算得到 $K = {Y_b}^{X_a} \mod p$
- B 通过计算得到 $K = {Y_a}^{X_b} \mod p$
- 攻击者像获得 K,需要求解离散对数(计算上不可能)
报文鉴别
回顾安全需求:
- 保密性 Confidentiality:数据、系统(访问控制)
- 完整性 Integrity:防止未授权的修改
- 可用性 Availability:合法用户总是可以访问
- 可认证 Authentication
- 抗抵赖 Non-repudiation
报文鉴别 面临的威胁:
- 泄密
- 流量分析:第三方分析你的流量大小
- 修改内容:报文被中间人修改
- 破坏数据包收到的先后顺序
- 发送方不承认发送过某报文
- 冒名顶替
报文鉴别 的需求
- 保护报文的完整性(报文鉴别、防篡改):报文加密
- 验证发送者的身份:报文鉴别码 (MAC)
- 抗抵赖:Hash 函数
报文加密
- 对称密钥加密。攻击者不知道密码,就无法篡改信息。
- ✅ 保密性
- ✅ 一定程度报文鉴别
- 只能来源于对方(因为密钥只有双方知道)
- 防篡改(需要配合冗余/特定格式)
- ❌ 不提供抗抵赖。双方有对称密钥,接受者有能力伪造报文。
- 公开密钥密码系统:用对方的公钥加密报文
- ✅ 保密性
- ❌ 报文鉴别、抗抵赖。因为中间人可以根据公钥加密并发送伪造信息。
- 公开密钥密码系统。私钥加密报文,对方用公钥解密。
- ❌ 保密性。因为任何人都有公钥。
- ✅ 完整性(防篡改)、抗抵赖。中间人无法用私钥加密,并保证其可以被公钥解开。
- 公开密钥密码系统。发送者用私钥加密,然后用接受者的公钥再次加密
- ✅ 保密性、完整性、抗抵赖
- 缺点是加密两次
报文鉴别码(MAC, Message Authentication Code)
- 报文加密的缺点:开销大、较难自动化
- 固定长度的比特串(如128bit)
- 由MAC算法生成
- 输入:报文和密钥
- 类似对称密钥
- 附加到报文上,用于报文鉴别
- 接受者做一样的检查,从而确保:
- 报文来自发送者
- 报文未被篡改
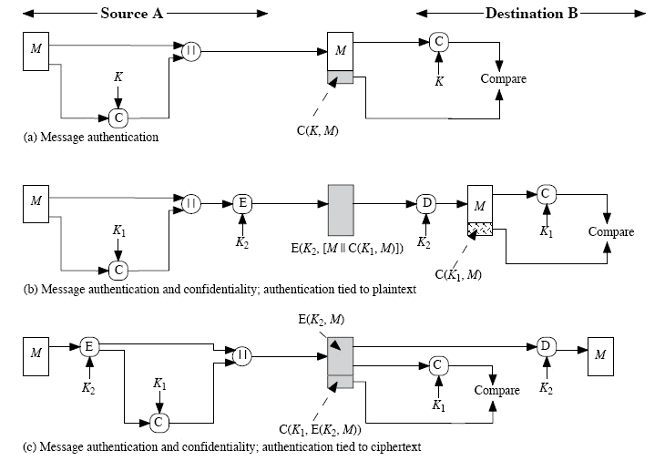
用法a(图):
- ❌ 保密性
- ✅ 完整性、验证发送者身份
- ❌ 抗抵赖:因为 K 是双方共享的
用法b,先 mac,然后用另一个对称密钥系统做加密
- ✅ 保密性
- ✅ 完整性、验证发送者身份
- ❌ 抗抵赖:因为 K1 和 K2 是双方共享的
用法c,先用对称密钥系统加密,然后 mac
- ✅ 保密性
- ✅ 完整性、验证发送者身份
- ❌ 抗抵赖:因为 K1 和 K2 是双方共享的
MAC 的性质(要求)mac = $C_K(M)$
- M 可变
- 使用密钥 K
- 输出固定长度的 mac
- 必然是一个多对一的函数
- 攻击:找到另一个 $M’$ 使得 $C_K(M’)=C_K(M)$,为了防止攻击,要求:
- 知道 mac,找到另一个 mac 值相同的报文非常困难
- MAC 应当是均匀分布的
- MAC 应当取决于报文的每一位
- 有哪些 MAC 生成算法
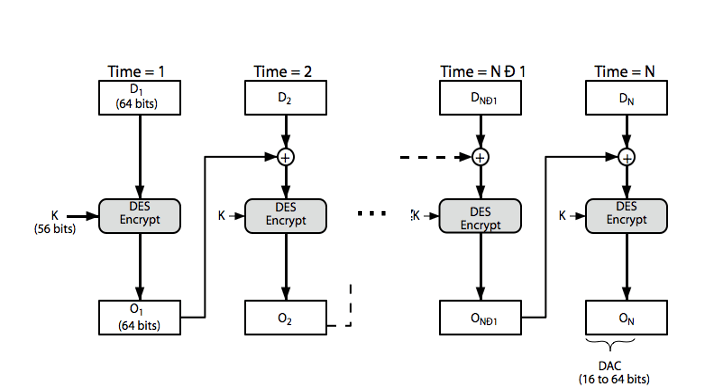
- 分组密码的 CBC(Cipher Block Chaining)模式的最后一个密文块作为 MAC
- Data Authentication Algorithm(DAA)是一个早期 MAC 生成算法,它基于 DES-CBC。 但是 MAC 太短(16-64个bit),不够安全
- 分组密码的 CBC(Cipher Block Chaining)模式的最后一个密文块作为 MAC
Hash 函数
Hash函数本身不使用密钥,并且是公开的
- 可以防止传输错误
- 无法防止恶意篡改,因为攻击者可能把 Hash 值一起改了
- 要用 Hash + 数字签名系统才可以防止恶意篡改
对 Hash 算法的攻击,叫做 Hash 碰撞攻击
- 单向性:已知 h,无法计算得到 x,使得 $h=H(m)$
- 弱抗碰撞性,给定 x,找到y,使得 $H(x) = H(y)$ 是计算上不可行的
- 强抗碰撞性,找到任意 x,y,使得 $H(x) = H(y)$ 是计算上不可行的
Hash的用法(参考下图)
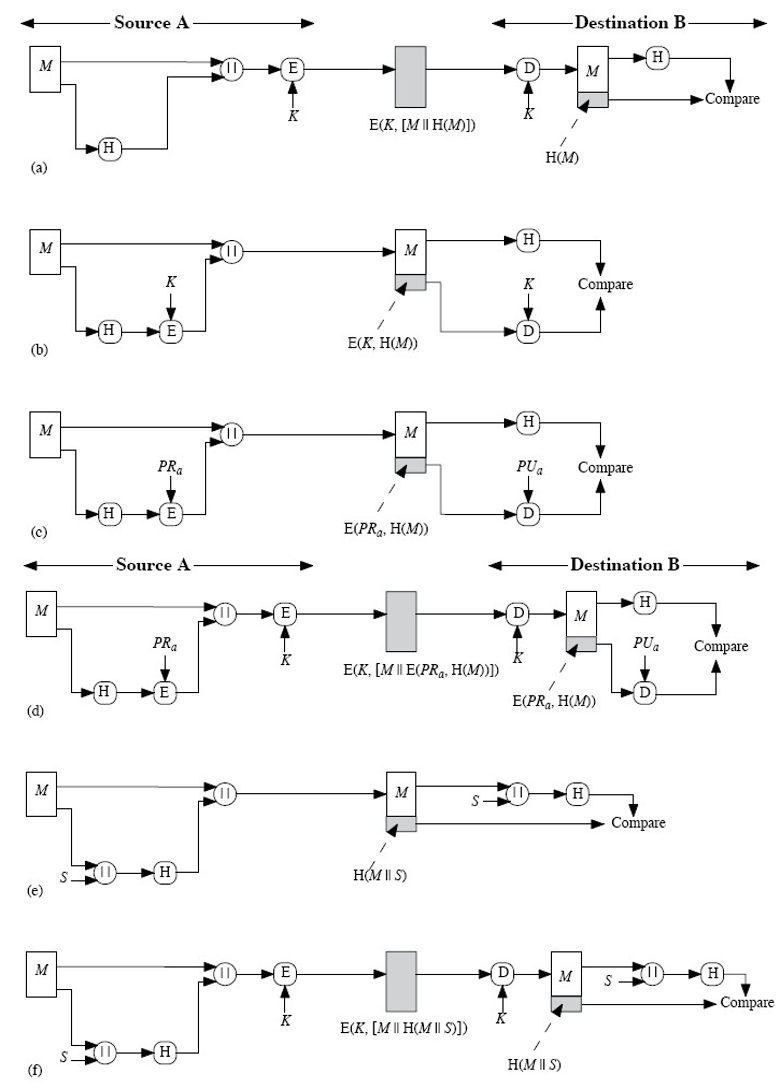
这 6 种用法的解释:
- 【a】配合对称加密系统,对全文加密,可以提供保密性、完整性、身份验证。需要共享密钥,不提供不可抵赖性。
- 【b】配合对称加密系统,对Hash值加密。(前面写的报文鉴别码)。提供安全性、身份验证。
- 【c】配合公钥加密系统,用私钥对Hash值加密,接收方用公钥对Hash值解密,然后对比。完整性、身份验证、抗抵赖。
- 【d】:在 【c】的基础上,传输前加密。
- 【e】:图中的 s 是一个随机数,这种用法常见于口令文件的保护。
- 【f】:在【e】的基础上,传输前加密
接下来介绍一些 Hash 算法
最简单的 Hash 函数:对报文分组异或
- 可以防止随机比特错误,但不能防止蓄意破坏
MD5
- Ronald 设计(他也是 RSA 的设计者之一)
- 系列算法 MD2,MD4
- 128bit哈希值
- 成为 Internet 标准 RFC1321
- 200x年起,有一些碰撞攻击的进展
SHA
- NIST和NSA与1993年设计(美国国标)
- 1995年修订为 SHA-1
- Internet 标准 RFC3174
- 基于 MD4
- 160bit哈希值
- 2005年后,有一些碰撞攻击的进展
- 之后开发了 SHA-256, SHA-384,SHA-512
- 它们与 AES 兼容
RIPEMD-160
- 欧洲开发
- 160bit哈希值
- 比 SHA-1 慢,更安全
生日攻击
- 生日悖论:一个班级,至少2个人生日相同的概率是多少?23个人是50%,30个人是70%
- 推广:如果有 $N$ 种可能,$n$ 个人随机选择他们,那么相同(碰撞)的概率约等于 $P \approx 1 - e^{-n^2/(2N)}$
- 如果 $n=\sqrt N$,那么 $P \approx 1/2$
- 也就是说,如果我们有 $\sqrt N$ 个报文,那么匹配的可能性为 50%
- 生日悖论的原因 是:我们不是找给定某个人的同生日概率,而是找一批人种任意两个同生日的概率
- 假设哈希值为 128-bit,那么列表长度为 $2^{64} \approx 10^{19}$ 即可发生 50% 概率碰撞
PKI
PKI(公开密钥基础设施,Public Key Infrastructure)
为什么?
- 中间人攻击:中间人用自己的公钥来伪造(替换)A的公钥。这样B以为在与A通信,实际上是在与中间人通信。
- 以上问题的核心:为什么要相信某个公钥,确实是某个人的公钥
- 解决方案:通过 证书(certificate) 来把公钥和身份关联在一起
- 证书由由公信力的第三方 CA(Certification Authority) 来证明
- 同时还可以提供其它功能:密钥生命周期、密钥如何获取
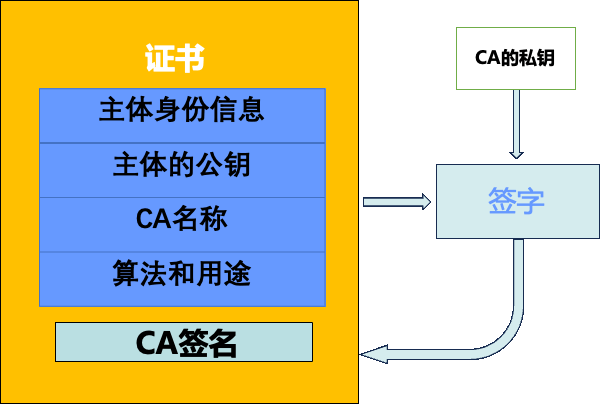
一个完整的PKI应该包括
- 证书授权中心(CA)
- 证书库
- 证书注销
- 密钥备份和恢复
- 自动密钥更新
- 密钥历史档案
- 交叉认证
- 支持不可否认
- 时间戳
- 客户端软件
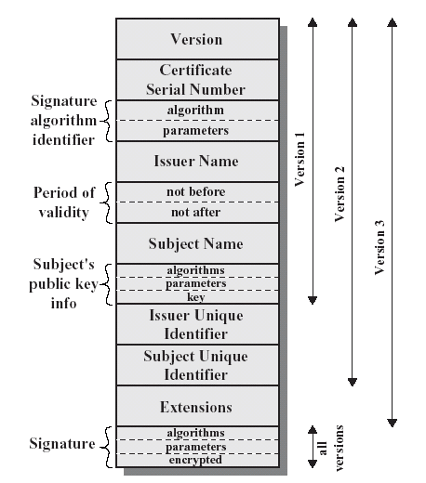
常见证书格式标准为 X.509 v3
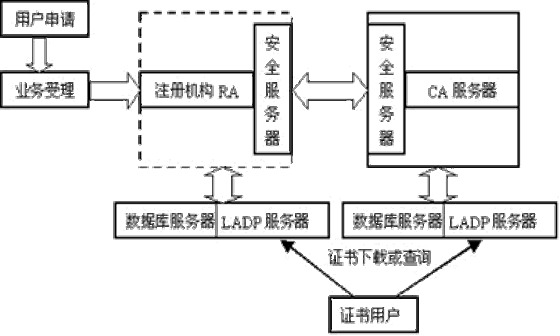
CA系统职责
- 接受用户的请求
- (由RA负责对用户的身份信息进行验证)
- 用自己的私钥签发证书
- 提供证书查询
- 接受证书注销请求
- 提供证书注销表
CA系统组成
- RA(Registration Authority)
- 用户和CA之间
- 接受用户的注册申请,收集用户信息和确认用户身份,对用户进行资格审查,决定是否同意CA给其签发数字证书并向CA提出证书请求
- 向LDAP服务器和安全服务器转发CA颁发的数字证书和证书撤消列表。
- CA(Certificate Authority)
- 发证
- 证书库/目录
- 保存证书,供公开访问
- LDAP服务器
- 提供目录浏览服务,将 RA 传输过来的用户信息以及数字证书加入到服务器上。这样其他用户通过访问LDAP服务器就能够得到其他用户的数字证书。
- 安全服务器
- 面向普通用户,
- 提供证书申请、浏览、证书撤消列表、证书下载等安全服务
证书注销:维护一个证书注销列表CRL(Certificate Revocation List)
- 标准:X.509 V2
- 延迟可能有 24小时
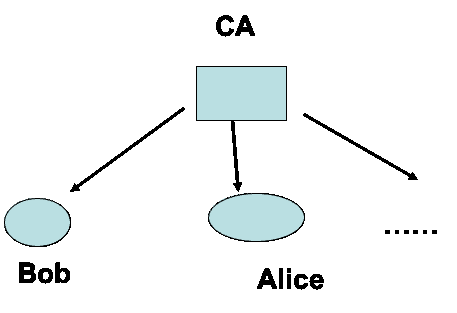
多个CA结构
层次结构CA
CA层次结构的建立
- 根CA具有一个自签名的证书
- 每个节点依次对子节点CA进行签名
- 叶子节点上的CA用于对安全主体进行签名
- 对于主体而言,它只需信任根CA (不关心中间的CA);同时它的证书是由底层的 CA 签发的
- 在CA的机构中,要维护这棵树
- 在每个节点CA上,需要保存两种cert
- Forward Certificates: 其他CA发给它的certs
- Reverse Certificates: 它发给其他CA的certs
层次结构CA中证书的验证
- 假设主体A看到B的一个证书
- B的证书中含有签发该证书的CA的信息
- 从 B 的 CA 开始,沿着层次树往上找,可以构成一条证书链,直到根证书
- 验证过程:
- 沿相反的方向,从根证书开始,依次往下验证每一个证书中的签名。其中,根证书是自签名的,用它自己 的公钥进行验证
- 一直到验证B的证书中的签名
- 如果所有的签名验证都通过,则A可以确定所有的证书都是正确的,如果他信任根CA,则他可以相信B的证 书和公钥
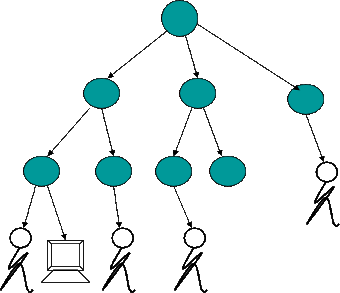
交叉结构CA
- 一个CA向另一个CA签发证书
- 可以单向签发,也可以互相签发
- 约束
- 限定名字
- 路径长度。可以让太长的路径失效
- 策略
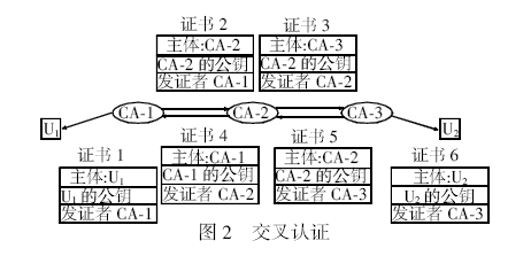
其它结构CA
身份认证
身份认证(Authentication)定义:
- 宣称者向验证者出示证据,证明其身份
- 至少2个参与者
- 是一种协议
- 分为单向认证、双向认证
- 最大的威胁:重放攻击
安全性排序
- 【弱】基于口令
- 【半强】基于动态口令
- 【强】基于密码技术
- 基于可信第三方:不但实现身份认证,还解决密钥分发问题
- Needham-Schroeder 协议
- Kerberos 协议
基于口令的身份认证
- 口令做 Hash 后存放
- 加盐
字典攻击。字典是人们常用的密码,或者已经泄漏的其他密码数据库
- 在线字典攻击:攻击者在网站上一个一个去试。很慢。
- 离线字典攻击:假设攻击者已经盗取了 Hash 值表,可以用密码字典去比较,从而得到密码
- 加盐大大提高攻击成本。因为攻击者需要把字典中的每个密码,与每个盐值结合起来才能计算 md5
Unix的做法
- 用 DES 做 Hash 函数
- 加盐,盐取决于系统时间
- 具体做法:salt 值+密码+其它信息拼接起来,然后整体做 Hash
- 这个 salt 值与口令文件(含Hash值的那个文件),一起存放
- 身份认证过程:先查询 salt 值,然后计算 md5,进而比对
动态口令(One Time Password, OTP)
- 最早是 Lamppost 动态口令方案(1981年)
- 事先分享一组口令序列,按照顺序使用
- 一组口令的生成:
h[t+1] = Hash(h[t]) - B 仅知道
h[N] - A 从 N-1 开始使用,按照
h[N-1], h[N-2], ..., h[1]的顺序使用它 - 每次 A 给 B 出示口令后,B 做 1次 Hash,即可验证。B 验证后
h[k]后,保存h[k+1]
评价:
- 可以防止重放攻击(replay attack)
- 但是不能防止 预先播放(Pre-play attack)攻击。就是攻击者获取了一组口令。
- 口令更新的时间窗口(1分钟、30秒)内还是会有重放攻击
- 用很多次后,需要重新初始化。成本很高。
- 不支持双向认证,没法确定口令给到了真正的 B
基于对称密码的身份认证
质询与应答(Challenge-Response)基本逻辑。假设B要完成对A的身份认证
- 身份认证基于 A 知道的某个秘密(如密钥)
- 首先 B 发给 A 一个随机数(Challenge)(有时候叫做 Nonce, Number used ONCE)
- A 收到随机数后,对它做某种变换,得到 Response,并把它发送回去
- Response 同时依赖随机数和 A 知道的秘密
- 构造的算法是此协议的核心
- B 收到 Response,验证 A 是知道这个秘密的
实现方式
- 对称密钥
- 对称密钥加密
- 报文鉴别码
- 非对称密钥
- 数字签名

基于对称密钥的单向身份认证 算法过程
- Challenge 是随机数
- 每次不同(符合 One Time Password),- ✅ 用来防止重放攻击
- 双方共享秘密 KA,Alice 使用 KA 加密 “Challenge + B”
- 为什么要连同 B 一起加密?为了抗 反射攻击(Reflection Attack)
- 假设没有连同 B 加密,并且是双向身份认证系统,就可以实施反射攻击:
- 攻击者用相同的随机数去质询 B,B 就会返回加密后的信息。而这段信息与 B 质询 A 的所需要返回的正确信息一模一样。
- 加入目标信息 B 之后,加密文本对应的明文就有目标信息,B 发现目标信息不对,就不响应。
- Bob Server 使用 KA 解密,然后比对随机数是否一致

基于对称密钥的单向身份认证2:基于时间戳 一个更简洁的算法
- 算法流程基本相同,只是不再使用随机数,而是时间戳
- B 比对返回的时间戳,与本地时间戳的误差是否可以接受

基于对称密钥的双向身份认证
- Bob 给 Alice 发送 Challenge (随机数 rb)
- A 返回的加密内容中,不但有 rb,还有自己生成的随机数 ra
- B 返回加密后的 ra, rb
【评价】基于对称密钥的身份认证:
- 需要双方共享密钥
- 密钥如何分发?如何管理?尤其是大规模、分布式系统中
基于报文鉴别码的身份认证
基于报文鉴别码(MAC)的身份认证,有两个经典协议
- SKID2(单向)
- SKID3(双向)
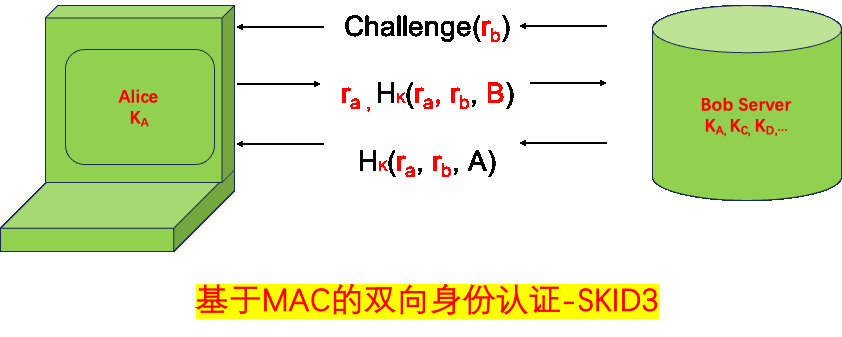
与前面的“基于对称密码的身份认证”基本类似,只是把加密函数,换成了哈希函数。
基于公钥系统的身份认证
基于公钥系统的单向身份认证 算法流程
- Bob -> Alice:
r_B(随机数) - Alice -> Bob:
cert_A, r_A, B, S(r_A, r_B, B)cert_A是 A 的签名证书,配合 PKI,可以获取到 A 的公钥B标记报文方向,防止 “反射攻击”(前面介绍过)r_A放到签名块中,是为了防止 选择文本攻击(chosen-text attacks)- 如果不加
r_A,攻击者用假的信息让 Alice 签名,从而获得假的签名
- 如果不加
基于公钥系统的双向身份认证 算法流程
- Bob -> Alice:
r_B(随机数) - Alice -> Bob:
cert_A, r_A, B, S(r_A, r_B, B) - Bob -> Alice:
cert_B, A, S(r_A, r_B, A)
还可以基于时间戳
一些典型的身份认证协议
Needham-Schroeder 协议
- 基于对称密钥的身份认证,密钥分发是个问题
- 假设有 n 个参与者,那么就需要 $n(n-1)/2$ 个对称密钥
- Needham-Schroeder 协议 就是为了解决这个问题
- 它使用 可信第三方 来解决这个问题
- 每参与者与可信第三方共享密钥即可,共需要 $n$ 个对称密钥
- 两个参与者需要的对称密钥(称为会话密钥,session key),在需要时由可信第三方来分发
- 通信完成后,丢弃会话密钥
Needham-Schroeder 协议
- 1978年提出
- 既解决密钥分发问题,也解决身份认证问题
- 这个协议有一些问题,中间人如果拿到历史的会话密钥,可以实施攻击。
- 这个协议不断改进,最终演化为 Kerberos 协议
Kerberos协议
- 经过长期考验。
- 80年代中期,MIT提出
- 解决的问题:认证、完整性、保密性
- 使用在分布式环境,C/S模型,服务器与用户之间的双向认证
- 使用对称加密(DES)
- 也是基于可信第三方的
- 处理三种威胁
- 用户伪装成另一个用户
- 攻击者把自己的地址伪造成另一个用户的
- 用户窃听报文,利用重放攻击进入服务器
一些符号
- C = 客户
- AS = 认证服务器(存放所有用户和用户口令)
- V = 应用服务器,有很多,为了解释简单,只描述一个
- IDc = C 上用户的标识符
- IDv = V 上用户的标识符
- Pc = C 上的用户口令
- ADc = C 的网络地址
- Kv = AS 和 V 共享的加密密钥
简单的认证对话
-
C -> AS: IDc Pc IDv - AS -> C: Ticket
-
Ticket = E_Kv(IDc ADc IDv)
-
-
C -> V: IDc Ticket
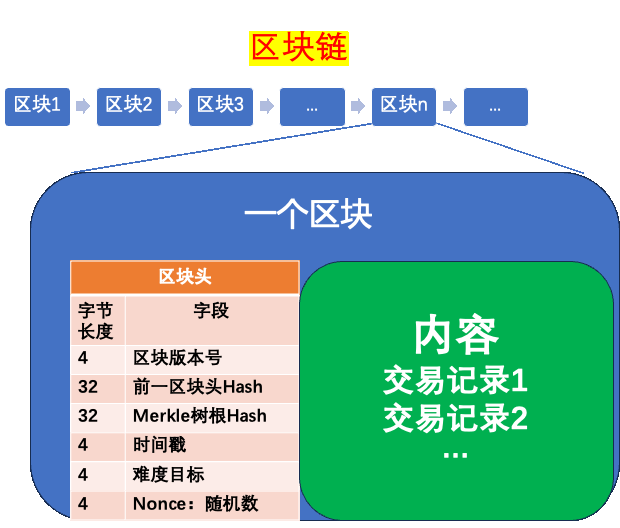
区块链
区块链是密码学技术(和P2P网络)的集大成应用
去中心化机制
- 账本公开
- 账本不记录余额,而只记录每笔交易
- 任何参与者都有一份账本
- 基本假设:一半以上的人诚实守信。即使少部分人伪造账本,真账本也不会被替代
- 区块
- 每个区块都是账本
- 最重要的是完整性
- 交易历史的完整性
- 交易本身的完整性
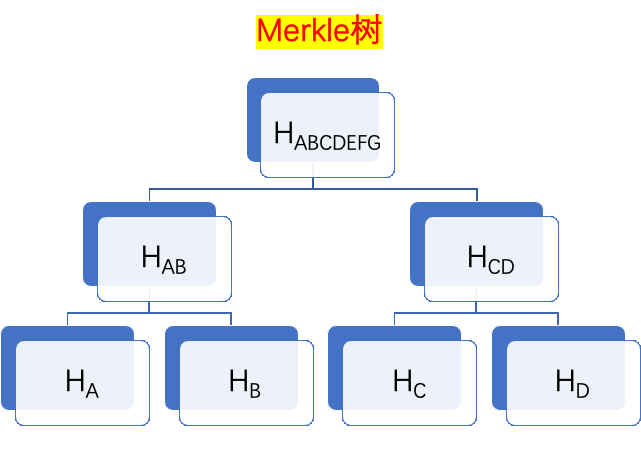
Merkle树:是一种 Hash 二叉树,用于快速归纳和校验大规模数据完整性
- 这个树本身不存储在区块中。只有根本存储在区块中(具体来说,区块头)。而各个子节点呢?可以根据本区块的交易记录来计算。
- 检查某元素是否在树中的性能是 $\log N$
- 使用两次
SHA256(叫做 double-SHA256) - 参考下面的图解释
- 构造树
- 假设两次 SHA256 操作,记为
DHash(input) = SHA256(SHA256(input)) H_A = DHash(A)H_AB = DHash(H_A, H_B)H_ABCD = DHash(H_AB, H_CD)
- 假设两次 SHA256 操作,记为
- 查询,假设需要查询
A是否在树中- 先计算
H_A,查询其兄弟节点,得到H_B,进而计算得到H_AB - 然后查询
H_AB的兄弟节点,计算得到父节点 - 直到得到根节点的 Hash 值,完成查询
- 先计算
谁来记账:矿工
- 挖矿过程:把最近交易记录记录在账本上(生成区块,并加入链条)
- 矿工有一定可能获得报酬
- 矿工可以随时退出,随时加入(P2P的特性)
- 挖矿有难度(有一定计算量),矿工之间有竞争关系
矿工的工作
- 收集交易单
- 付款人把交易单给到收款人,同时投递到矿工小组的收件箱中
- 矿工定期把交易单取出
- 填写账本
- 填写区块头
- 按比填写交易记录
- 工作量证明(Proof-of-work)
- 新区块被别的矿工认可:别的矿工开始在这个区块上计算下一个区块
- 新区块头的 HASH 必须满足计算量的要求。矿工需要找到一个合适的随机数 Nonce,使其满足
H(头) = 0x00..00FF..FFF(共64位16进制) ,其中F的个数取决于 难度值- 计算很难,验证很简单
- 难度值动态变化,每2016个区块更新一次。目的是使区块的生成速度不能太快,使其平均在10分钟左右
共识机制:与工作量证明一起,保证完整性
- 报酬:每个矿工的交易清单第一笔交易,就是“系统向本矿工支付50个比特币”
- 最早是50个比特币,规定每 210,000 个区块减半一次,2025年已经衰减到 3.125BTC 了
- 因此,比特币最多就 2100万个
- 除了固定奖励,还有该区块所有交易的手续费(通常0.1-0.5BTC)作为报酬
- 最早是50个比特币,规定每 210,000 个区块减半一次,2025年已经衰减到 3.125BTC 了
- 矿工完成计算后,立即请求别的矿工确认
- 所有矿工收到新区块时,立即停止挖矿并确认
- Hash 是否满足难度值要求
- 前一个区块确实是自己的最后一个区块,且 Hash 正确
- 交易清单有效:付款人有余额
- 新区块被别的矿工认可:别的矿工开始在这个区块上计算下一个区块
问题讨论
问题1:同时收到2个合法区块
- 由于矿工们是并行的,完全可能同时收到两个合法的新区块
- 答:不以线形方式组织账本,而是树状,任何时刻以当前最长分支位主账本,但保留其它分支
- 规定:收款人在公告挂出后不能立即确认交易完成,而是再等待6个区块,并且之前的区块没有被取消
- Proof-of-work,正是为了防御 伪造区块攻击,它在落后6个区块的情况下,赶超主分支非常困难。需要算力超过所有其它算力之和
问题2:通货膨胀
- 挖矿报酬不能一直进行下去,而是(前面提到的)减半
- 一旦挖完,挖矿报酬就只有手续费
问题3:防篡改 Hash(double-SHA256)来保证
- 攻击1:改变区块内的交易记录,那么 Merkle 根对不上
- 攻击2:改变交易记录和 Merkle 根,那么区块 Hash 对不上
- 攻击3:攻击者没有达到难度就提交区块,用公式很容易验证
- 攻击4:攻击者改变区块内容、区块Hash,那么本区块的下一个区块头保存的
prev_hash对不上 - 攻击5:攻击者掌握51%以上算力,那么确实可以修改所有区块,这他做合法公民的收益更大、更安全
交易记录:公钥系统实现身份标识+交易签名
- 交易记录中的内容
- 唯一编号
- 交易内容
- 付款人的签名:
E_付款人的SK(当前交易 + 收款人的 PK)
- 如何验证一笔交易
- 验证签名
- 验证交易的钱大于余额
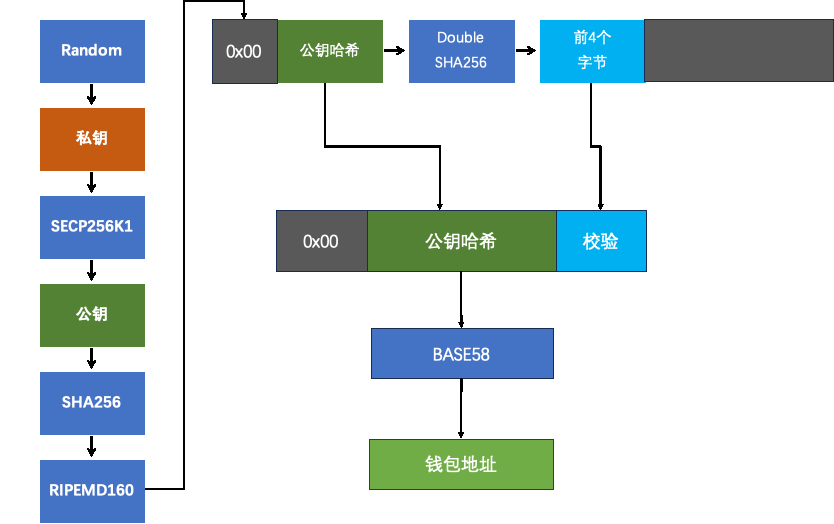
关于钱包地址、公钥、私钥之间的关系,
- SECP256K1 算法(基于 ECC),算法强度强、公钥长度短
隐私保护
- 账本公开,是否某比特币拥有者的账目都查出来了?
- 不是,每次交易使用不同的公钥,就查不到同一个人的所有账目了
防火墙
找到关键节点(路由)
防火墙能为我们做什么
- 访问控制
- 服务控制:确定哪些服务可以被访问
- 方向控制:确定哪个方向可以通过防火墙
- 用户控制:哪些用户可以访问
- 行为控制:控制特定服务的行为
- 监视个字安全时间,审计、报警
- 其它功能:地址转换、Internet 日志、审计、计费
- IPSec 实现平台
- 不能做什么
- 绕过防火墙的行为。内部拨号、VPN、用http协议虚拟一个tcp-ip协议
- 内部的攻击
- 不能过滤带病毒稳文件
- 性能影响
参考
您的支持将鼓励我继续创作!
