🔥 数据库原理 | 郭飞的笔记

数据库的总揽

数据库：将信息规范化、电子化，而形成的库，以便快速有效的存储、检索、统计、管理

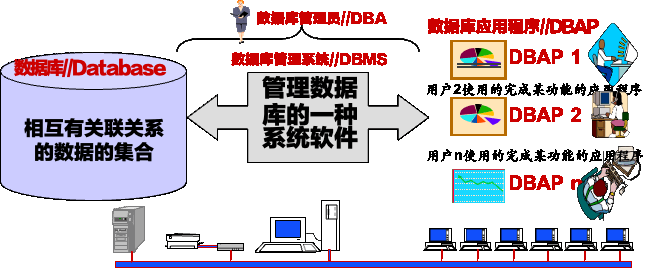
数据库系统，包括：

数据库（DB，Database）
数据库管理系统（DBMS，Database Management System）
数据库应用（DBAP，Database Application）
数据库管理员（DBA，Database Administrator）
计算机基本系统

caption: 数据库系统

数据库管理系统，应该有什么功能？（用户角度）

数据库定义
- DBMS 提供 数据定义语言（DDL，Data Definition Language）给用户
- 用户使用 DDL 描述表格式
- DBMS 按照用户描述，创建数据库和其中的 Table
数据库操纵
- DBMS 提供 数据操纵语言（DML，Data Manipulation Language）
- 用户使用 DML 描述所要进行的增、删、改、查等操作
- DBMS 按照用户描述，执行这些操作
数据库使用
- DBMS 提供 数据控制语言（DCL，Data Control Language）
- 用户使用 DCL 描述其对数据库要实施的控制（用户访问权限）
- DBMS 按照用户的描述，实际进行控制
数据库维护
- DBMS 提供一系列程序给用户，这些程序提供了对数据库维护的各种功能
- 用户使用这些程序对数据库维护
- 数据库维护程序，一般由 DBA 使用和掌握

数据库管理系统，应该有什么功能？（系统角度）

语言编译器。把数据库语言，翻译成 DBMS 可执行的命令。如 DDL 编译器，DML 编译器，DCL 编译器
查询优化、查询实现。提高检索速度
数据库的存取、索引。提供在磁盘、磁带上的高效存取手段
通信控制。网络环境下的数据库操作与数据传输手段
事务管理。高可靠性，避免并发操作错误
故障恢复。数据库自动回复到故障发生前正确状态的手段。如备份、运行日志
安全性控制。避免非授权用户访问数据库
完整性控制。提供数据、数据操作正确性检查手段
数据字典管理。管理用户定义的信息
应用程序接口（API）：提供应用程序使用 DBMS 特定功能的手段
数据库数据装载、重组
数据库性能分析。统计运行过程中的各种性能数据，以便优化。

典型的 DBMS：

Oracle
MS SQL
…

数据库系统的结构抽象

DBMS 管理数据的三个层次

External level（User level）。某一用户能够看到的数据，是全局数据的某一部分
Conceptual level（Logic level）。全局角度理解的数据
Internal level（Physical level）。存储在介质上的数据，含路径、存储方式、索引方式等

数据和模式的区别

数据（View/Data）。是数据本身。
模式（Schema）。数据的结构性信息。例如： table_student(id char(8), name char(10))

三级模式（对应上面的3个层次）

External Schema。同义词：用户模式、外模式、局部模式
Conceptual Schema。模式默认指的是 Conceptual Schema。同义词：全局模式、概念模式、逻辑模式
Internal Schema。同义词：内模式、存储模式

两层映像

E-C Mapping。External Schema 到 Conceptual Schema 的映射
C-I Mapping。Conceptual Schema 到 Internal Schema 的映射

为什么要这样设计？

逻辑数据独立性。Conceptual Schema 变化时，可以不改变 External Schema，只需要改动 E-C Mapping
物理数据独立性。Internal Schema 变化时，可以不改变 Conceptual Schema，只需要改动 C-I Mapping

数据模型：

规定统一描述方式，包括数据结构、操作、约束。
“数据模型”是“数据模式”的抽象，“数据模式”是数据本身的抽象
3种经典数据模型：
- 关系模型：表的形式组织数据
- 层次模型：树的形式组织数据
- 网状模型：图的形式组织数据

数据库的演变

从文件系统到数据库
- 文件系统的优点：用户（程序）不必考虑物理细节
- 缺点：数据与程序耦合，需要在程序中定义数据的组织。
- 因此需要一个专门的 DBMS 专门处理数据
从层次模型、网状模型，到关系数据库
- 层次模型、网状模型，数据是用指针联系起来的，只能逐一操作。
- 关系数据库不依赖指针、路径，理论基础完善
关系数据库到对象数据库
- 关系第一范式：每个单元格只能有1个值
- 对象关系数据库：使用数据结构/面向对象特点，来封装那些不满足关系第一范式的数据（一个单元格有多行/多列的情况）。
- XML数据库：半结构化数据库，把数据和数据的语义合并存储。是一种树型的数据组织形式。
ODBC（Open Database Connection）/（Java 对应的是 JDBC）：一种数据库标准，可以让应用程序用统一的方式访问不同的数据库
新型数据库。在不同的领域，有不同的数据库。例如：与实时技术结合的实时数据库，与工程文件结合的工程数据库，与图像结合的图像数据库

关系数据库

关系模型三要素

基本结构：Relation/Table
操作（Relation Operator）
- 基本操作：并（Union）、差（Difference）、广义积（Product）、选择（Selection）、投影（Projection）
- 扩展操作：交（intersection）、连接（join）、除（Division）
完整性约束：实体完整性、参照完整性、用户自定义完整性

关系数据库：操作的对象是集合，一次一集合（Set-at-a-time）。层次模式、网状模型：操作对象是一次一记录（Record-at-a-time）

一些定义

Domain（域）：列的取值范围集合，例如，性别这个字段的域就是 {男, 女}

Cardinality（基数）：集合的元素个数

Cartesian Product（笛卡尔积），所有可能性的集合：

一组域 $D_1,D_2,…,D_n$ 的笛卡尔积是：$D_1 \times D_2 \times ... \times D_n =\{ (d_1,d_2,...,d_n) \mid d_i \in D_i, i=1,...,n \}$
每个元素 $(d_1,d_2,…,d_n)$ 叫做 n-元组（n-tuple）
元组的每个值 $d_i$ 叫做 分量（component）

关系（Relation）：$D_1 \times D_2 \times … \times D_n$ 的一个子集

Schema 用 $R(A_1:D_1, A_2:D_2,…,A_n:D_n)$ 表示

其中 R 是关系的名字
$A_i$ 是属性名字
$D_i$ 是域
n 是关系的 degree（度、目）
例如 Student(S# char(8), Sname char(10), Ssex char(2), Sage integer)

关系的特性

列是同质的：数据类型相同（来自同一个域）
列名必须不同（$A_i$ 不同）
列位置可互换，行位置可互换。不靠位置索引号确定行/列。行/列互换后，仍然是同一个关系。
理论上，关系任意两个元组不能完全相同（因为它是集合）。实践上不一定完全遵守。
属性不可再分：关系第一范式
Candidate Key（候选码、候选键）：关系中的一组属性，其值可以唯一标识一个元组。例如 学生(S#,Sname,Sage,Sclass) 中的 S# 是候选码；选课记录(S#,C#,Sname,Cname,Grade) 中的 (S#,C#) 是候选码。
- 当然，候选码可以有多种，可以选定其中的一个作为主码，例如上面选课记录中的 (S#,C#)
- 任何候选码中都有的属性叫做 主属性，例如上面的 C# 和 S#，其它都是 非主属性
- 最简单的：候选码只有一个属性。最极端的：全部属性都是主属性（成为全码 All-Key）
Foreign Key（外码/外键）：关系R的一个属性组，它不是R的候选码，但它是另一关系 S 的候选码。
- 例如：“合同”关系中的“客户号”不是候选码，但它是“客户”关系中的候选码
- 两个关系靠外码连接起来

caption: 第一范式

完整性

实体完整性：主码的值不能为空值
参照完整性：如果 R1的外码 Fk 与 R2 的主码 Fk 对应，那么 R1 的每个元组的 Fk 值，要么等于 R2 某元组的 Pk 值，要么为空。
- 举例来说，“学生”表的外码“班级号”，与“班级”表的主码“班级号”对应，那么每个学生的“班级号”，要么在“班级”表中有，要么为空（为空可能是还没给他分班）。换句话说，一个学生不可能被分到一个不存在的班里。
用户自定义完整性：用户要求某个字段在约束范围内。例如年龄要大于0小于200；例如性别只有男/女

关系代数

关系代数：以集合为中心的运算，操作的对象是集合，操作的结果也是集合

关系代数基本操作：并、差、积、选择、投影
关系代数扩展操作：交、theta-连接、自然连接
关系代数复杂扩展操作：除、外连接

并（union）

前提：关系 R 和关系 S 有相容性。

关系 R 和关系 S 有 相容性，假设 R(A1, A2,... An)，S(B1, B2,..., Bm)

R 和 S 的属性数目相同，即 n = m
对于任意的 i，Ai 和 Bi 的域相同

举例，这两个关系是相容的：STUDENT(SID char(10), Sname char(8), Age char(3)) 和 PROFESSOR(PID char(10), Pname char(8), Age char(3))

并操作的定义：R和S是相容的，那么 $R \cup S = \{ t \mid t\in R \lor t \in S\}$

解释：实际上就是 SQL 中的 UNION

差（Difference）

定义：前提是 R 和 S 是相容的，那么 $R - S = \{ t \mid t\in R \lor t \not\in S\}$

笛卡尔积（Cartesian Product）

定义：R 和 S 中元组的所有可能的组合

用数学语言定义：$R \times S = \{ (a_1, a_2,..., a_n, b_1, b_2,..., b_n) \mid (a_1, a_2,..., a_n) \in R \land (b_1, b_2,..., b_n) \in S\}$

性质

可交换，$R \times S = S \times R$
如果 R 和 S 的属性个数为 n 和 m，那么 $R \times S$ 的属性个数为 n + m
如果 R 和 S 的基数分别为 x 和 y，那么 $R \times S$ 的基数为 n * m

选择（Select）

$\sigma_{con} (R) = \{ t \mid t \in R \land \mathrm{con}(t) = \mathrm{true} \}$

其中 con 是由一系列逻辑运算符、比较表达式组成的表达式

解释：就是 SQL 语句中的 WHERE

投影（Project）

定义：选出 R 中的一些属性，然后形成新的关系

数学描述: 假设 $R(A_1, A_2, …, A_n)$，那么 $\pi_{A_{i_1},A_{i_2},...A_{i_k}} = \{(t[A_{i_1}], t[A_{i_2}],..., t[A_{i_k}]) \mid t \in R\}$

其中，$\{A_{i_1},A_{i_2},...A_{i_k}\} \subseteq \{ A_1, A_2, ... , A_n\}$

解释：就是 SQL 语句中的 SELECT

交（Intersection）

定义：前提是 R 和 S 是相容的，那么 $R \cap S = \{ t \mid t\in R \land t \in S\}$

性质：$R \cap S = R - (R- S) = S - (S - R)$

theta-连接（theta-join， θ-join）

$R \mathop{\bowtie}\limits_{A \theta B} S = \sigma_{t[A] \theta s[B]}(R \times S)$

用语言描述就是：先做笛卡尔积，然后找出满足 $\theta$ 条件的那些元组（“选择”），形成一个新的关系
A 和 B 必须有可比性
$\theta$ 可以是 >, >=, <, <=, =, !=

caption: θ-连接

说明：

笛卡尔积是数学上的，在程序实现上不会先做笛卡尔积
最常见的是 等值连接 $R \mathop{\bowtie}\limits_{A = B} S = \sigma_{t[A] = s[B]}(R \times S)$

自然连接（Natural-Join）

是一种特殊的等值连接
其连接条件是，R和S相同的属性，其值相同
$R \bowtie S = \sigma_{t[B] = s[B]}(R \times S)$
其中 B 是一组名字相同的属性
最终的结果，需要去掉一个相同的属性（只保留一个）

除（Division） $R \div S$

前提：对于 $R(A_1, A2_,… A_n)$ 和 $S(B_1, B_2,…, B_m)$，$\{ B_1, B_2,..., B_m \} \subset \{A_1,A_2,...,A_n\}$，（也就是说，S 的属性集是 R 属性集的真子集，并且 $m < n$）

定义：

结果的属性，为 $\{C_1,C_2,...,C_k\} = \{A_1,A_2,...,A_n\} - \{ B_1, B_2,..., B_m \}$，其中 $k = n - m$
结果的元组，$(c_1,…,c_k)$ 应当满足：它与 S 中每个元组 $(b_1,…,b_m)$ 结合，形成的新元组，都是 R 中的元组 $(a_1,…,a_n)$

数学描述

集合语言描述：$R \div S = \{ t \mid t \in \pi_{R-S} \land (\forall u\in S \to tu \in R)\}$
关系代数描述：$R \div S = \pi_{R-S}(R) - \pi_{R-S}((\pi_{R-S}(R) \times S) - R)$

现实描述：R是学生选课表，S是课程表， $R \div S$ 查询出“选修了全部课程的学生”

外连接（Outer-Join）

left outer join（左外连接）：$R ⟕ S$
right outer join（右外连接）：$R ⟖ S$
full outer join （全外连接）：$R ⟗ S$

描述：在自然连接中，没有匹配上的元组都丢掉了，外连接使没有匹配上的元组不丢掉，而是把没匹配上的也加入进去，额外的字段设定为空值

还有一些运算不是经典代数的最基本的运算，但在查询优化中是基本运算

$\sigma(R)$ 去重 DISTINCT
$\gamma_{dept;AVG(salary)}(Employee)$ 分组聚合 GROUP BY dept
$\tau_A (R)$ 排序 ORDER BY A
集合上的并、交、补（去重）
包上的并、交、补（不去重）

关系元组演算

关系演算包括：

关系元组演算，以元组作为谓词变量
关系域演算，以域变量为谓词变量

关系元组演算定义：$\{ t \mid P(t) \}$

意思：所有谓词 P 为真的元组 t 的集合
t是元组
$t\in R$ 表示元组 t 在关系 R 中
$t[A]$ 表示 t 在属性 A 上的值
$P(t)$ 是公式，可以递归地构造

公式的定义：公式 $P(t)$ 可以递归地构造

三种原子公式
- $s\in R$
- $s[A] \theta c$
- $s[A] \theta u[B]$ （ $\theta$ 前面定义过了）
如果 $P$ 是公式，那么 $\lnot P$ 也是公式
如果 $P1,P2$ 是公式，那么 $P1 \land P2$ 和 $P1 \lor P2$ 也是公式
如果 $P(t)$ 是公式，$E$ 是关系，那么 $\exists (t\in R)(P(t))$ 和 $\forall (t\in R)(P(t))$ 也是公式
加括弧也是公式
运算符优先顺序：括弧、$\theta, \exists, \forall, \lnot, \land, \lor$
公式仅限以上形式

关系域演算

基本形式：$\{ (x_1, x_2,..., x_n) \mid P(x_1, x_2,..., x_n)\}$，它是以域为基本单位的。其定义与关系元组运算基本一样。

域演算语言（QBE，Query By Example）

1975年提出，1978年实现
这个语言是把查询条件写到表格中的
（太老了，这个语言，不细写了）

关系运算的观点

安全性：不产生无限关系和无穷验证的运算，叫做安全的

关系代数是一种集合运算，是安全的。
- 集合本身是有限的，运算次数是有限的，因此关系代数是有限的。
关系演算不一定安全
- $\{ t \mid \lnot R(t) \}$ 可能表示无限关系，因为不在 $R(t)$ 中的元素可能是无限的
- $\{ t \mid R(t) \lor t[2]>3 \}$ 不是安全的，因为 $t[2]>3$ 可能是无限的
- 安全约束：施加一个约束条件，使任何公式都在一个集合范围内操作（而不是无限范围）。安全约束有限集合 DOM

关系运算有3种：关系代数、关系元组演算、关系域演算

三种运算之间是等价的：关系代数、安全的元组演算表达式、安全的域演算表达式，三个是等价的
3种关系运算，是衡量 数据库语言完备性的基础

SQL

SQL 系列文章：

🔥【SQL】SELECT专题，主要内容是 SELECT 语句
【SQL】通用语法，主要内容是 CREATE、ALTER、INSERT 等通用的 SQL 语法
各种数据库方言，各种数据库的相关命令，如 HIVE、MySQL、SQL Server
【python】sqlAlchemy

数据库完整性

数据库完整性（DB Integrity）

广义完整性：语义完整性、并发控制、安全控制、故障恢复
狭义完整性：指的是语义完整性

关系模型中的完整性：

实体完整性
参照完整性
用户自定义完整性

引发完整性问题的原因：不正确的数据库操作：输入错误、操作失误、程序处理失误

如何应对：
- 防止数据库中出现不合理的数据
- DBMS 尽可能防止 DB 中的语义不合理现象
DBMS 如何保证完整性：
- DBMS 允许用户自定义约束规则（SQL-DDL）
- 有更新操作时，DBMS 先自动按完整性约束进行检查，然后更新数据库

完整性约束的一般形式： Integrity Constraint = (O, P, A, R)

O:数据集合（约束的对象），列、多列、元组等
- 按约束对象划分
  - 域完整新约束：给定列，其值要满足约束条件，例如规定 age 要在0-150之间
  - 关系完整性约束：某一元组要满足约束条件，或者若干元组与另一个关系若干元组一起满足约束条件，例如规定学时除以学分要在 6-7之间
- 按照约束来源分类
  - 结构约束：函数依赖、主键、外键、是否允许空值
  - 内容约束：用户自定义的范围，如 age
- 按照约束状态分
  - 静态约束：满足的固定条件，如一个范围
  - 动态约束：例如 age 只能升，不能降。用触发器实现
P:谓词条件（什么样的约束）
A:触发条件（什么时候检查）
R:相应动作（不满足时怎么办）

静态约束

静态约束用 CREATE 语句实现

CREATE TABLE tablename(
    colname1 datatype [ DEFAULT { default_constant | NULL} ]
        [ col_constr {col_constr. . .} ] -- 字段级别约束
    ,colname2 datatype
    ,...
    -- 以下是表级别约束
    ,table_constr1
    ,table_constr2
);


-- 字段级别约束的写法
{ NOT NULL |                               -- 列值非空
    [ CONSTRAINT constraintname]           -- 为约束命名，便于以后撤消
        { UNIQUE                           -- 列值是唯一
        | PRIMARY KEY                      -- 列为主键
        | CHECK (search_cond)              -- 列值满足条件，search_cond 的写法与 SQL 的 WHERE 写法一样，但只作用于单列
        | REFERENCES tablename [(colname) ] -- 列是外键，需要指定它是哪个表的主键
            [ON DELETE { CASCADE | SET NULL } ] } } -- 对应表的记录被删除时，这个表对应的行 删除/置为 NULL

-- 一个字段级约束例子：
CREATE Table Student ( 
    S# char(8) not null unique                           -- 列非空、唯一
    ,Sname char(10)
    ,Ssex char(2) 
        CONSTRAINT ctssex CHECK (Ssex=‘男’ or Ssex=‘女’) -- 约束的名字为 "ctssex"
    ,Sage integer CHECK (Sage>=1 and Sage<150)          -- 对 Sage 字段的约束
    ,D# char(2) REFERENCES Dept(D#) ON DELETE CASCADE   -- 它是外键，对应表 Dept 的 D# 字段，并且如果 Dept 的记录被删除，此表对应的记录也删除
    ,Sclass char(6)
);




-- 表级别约束的写法：
[CONSTRAINT constraintname] -- 为约束命名，便于以后撤消
    {UNIQUE (colname {, colname. . .})           -- 几列值组合在一起是唯一
    | PRIMARY KEY (colname {, colname. . .})     -- 几列联合为主键
    | CHECK (search_condition)                   -- 元组多列值共同满足条件
    | FOREIGN KEY (colname {, colname. . .})
        REFERENCES tablename [(colname {, colname. . .})]
        [ON DELETE CASCADE] }
        -- 引用另一表tablename的若干列的值作为外键


-- 一个表级别约束的例子：
Create Table Course (
    C# char(3)
    ,Cname char(12)
    ,Chours integer
    ,Credit float(1) CONSTRAINT ctcredit CHECK(Credit >=0.0 and Credit<=5.0)           -- 仍然可以做字段级别约束
    ,T# char(3)
    ,primary key(C#)       -- 表级别约束
    ,FOREIGN KEY(T#) REFERENCES Teacher(T#) ON DELETE CASCADE -- 表级别约束
    ,constraint ctcc check(Chours/Credit = 20)  --表级别约束
);

约束条件可以是 WHERE 之后的语句，例如：

CREATE TABLE SC(
    S# char(8) check( S# in (select S# from student)), -- 约束条件是一个子查询
),

ALTER TABLE 也有类似的用法（几乎与 CREATE 一样）：

ALTER TABLE tblname
    -- 增加列的同时，可以加入约束
    [ADD ( { colname datatype [DEFAULT {default_const|NULL} ]
        [col_constr {col_constr...} ] | , table_constr }
        {, colname ...}) ]
    -- 删除一个列
    [DROP { COLUMN columnname | (columnname {, columnname…})}] 
    -- 修改一个列的同时，修改其约束
    [MODIFY ( columnname data-type
        [DEFAULT {default_const | NULL } ] [ [ NOT ] NULL ]
        {,columnname . . .})]
    -- 增加一个约束
    [ADD CONSTRAINT constr_name]
    -- 删除一个约束
    [DROP CONSTRAINT constr_name]
    [DROP PRIMARY KEY];

-- 例子1：
ALTER TABLE SC DROP CONSTRAINT ctscore;

-- 例子2
ALTER TABLE SC
    MODIFY ( Score float(1) CONSTRAINT nctscore CHECK (Score>=0.0 and Score<=150.0) );

第二种约束的写法：断言（ASSERTION），格式为 CREATE ASSERTION <assertion-name> CHECK <predicate>，影响性能，用的不多，不写了。

动态约束

动态约束用 触发器（TRIGGER） 实现

CREATE TRIGGER trigger_name BEFORE | AFTER -- 事件发生前/后
    {INSERT | DELETE | UPDATE [OF colname {, colname...}]} -- 事件是什么
    ON tablename 
    [REFERENCING corr_name_def {, corr_name_def...} ]  -- 定义变更前后的变量名，方便在 statement 中使用
    [FOR EACH ROW | FOR EACH STATEMENT]    -- 对每一行，对每次操作
    [WHEN (search_condition)]              --检查条件，如满足执行下述程序
        {statement                         -- 执行单行程序，直接书写
        | BEGIN statement1; statement2;... END -- 如果执行多行语句，要加 BEGIN 和 END
        }

-- 一个例子：规定工资只能上调，不能下调
CREATE TRIGGER teacher_chgsal BEFORE  
    UPDATE OF salary
    ON table_teacher
    REFERENCING new x, old y -- 定义新/旧值，方便在下面使用
    FOR each ROW
    WHEN(x.salary < y.salary) -- 检查条件
    BEGIN
        -- statement 可以是一个 SQL-UPDATE/DELETE 等语句
        raise_application_error(-20003, 'invalid salary on update');
    END;

其它

-- 显示触发器
SHOW TRIGGERS;

-- 删除触发器
DROP TRIGGER trigger_name

数据库安全性

数据库安全性指的是DBMS应该保证数据库的一种特性：免受非法、非授权用户的使用、泄露、更改、破坏

DBMS 的安全机制

自主安全机制：用户自己做 Access Control，权限在用户之间传播
强制安全机制：对数据、用户分类分级，不同类别的用户可以访问不同类别的数据
推断控制：防止通过历史信息、公开信息，推断出私密信息
数据加密存储

自主安全机制，使用 SQL-DCL，规则是 Access Rule = (S, O, t, P)

S:请求主体（用户），也可以是用户组
O:访问对象，粒度可大可小，例如字段（属性）、记录（元组）、表（关系）、数据库
t:访问权利，创建、增、删、改、查
P:拥有权力需满足的条件，例如仅员工允许访问自己的数据

【例子】一个员工数据库，安全性要求：

员工管理人员：需要所有的读写权限
收发人员：访问员工、部门，不允许访问其它信息
每个员工：只允许访问自己的记录，可以查询工资
部门领导：查询所在部门所有人的情况

SQL-DCL

数据库权限分级（高等级自动包含低等级权限）：

SELECT：读
MODIFY：包括 INSERT、UPDATE、DELETE
CREATE：CREATE、ALTER、DROP

-- 授予权限
GRANT {ALL PRIVILEGES | privilege {,privilege…}}
ON [TABLE] tablename | viewname
TO {public | user-id {, user-id…}}
[WITH GRANT OPTION];         -- 是否允许该用户把权限授予另一个用户

-- 例子
GRANT select ON table_employee TO user1 WITH GRANT OPTION;
GRANT ALL PRIVILEGES ON table_employee TO user2;
GRANT select ON table_employee TO public;



-- 收回权限
REVOKE {all privilEges | priv {, priv…} } ON tablename | viewname
FROM {public | user {, user…} }

第二种访问控制手段：VIEW

嵌入式SQL

是什么？把 SQL 潜入到高级语言（C/C++/Java/Python）中

为什么？

复杂的查询，普通用户可能写不对
一些复杂的结果难以用一条 SQL 完成，
- 例如循环：Do While some-condition SQL-Query End Do
- IF 语句
- 在 SQL 结果上继续处理

C 语言为例：

EXEC SQL select Sname, Sage into :vSname, :vSage from Student
where Sname=‘张三’;

解释：

EXEC SQL: 把 SQL 预编译为 C 可识别的语句
增加 into 子句：把 SQL 检索结果，指定给 C 的变量

数据库的连接与断开，变量的声明与使用

// 连接数据库，下面是标准语法。每种数据库还提供不同的语法
EXEC SQL connect to sql_server_name as connect_name user user_name;

// 定义变量
EXEC SQL BEGIN DECLARE SECTION;
    char vSname[10], specName[10]="张三";
    int vSage;
EXEC SQL END DECLARE SECTION;

// SQL 语句
EXEC SQL SELECT name, age into :v_name, :v_age from
table_student where name= :specName;

// 最后断开连接（每种数据库提供不同的语法）
EXEC SQL disconnect connect-name;

事务

SQL 的提交与撤销

// 提交
EXEC SQL COMMIT WORK;

// 撤销
EXEC SQL ROLLBACK WORK;

为什么需要提交与撤销？

代码如何表示事务：可以用 Begin Transaction 和 End Transaction 把一个事务框起来。也可以由代码根据 EXEC SQL COMMIT/ROLLBACK WORK 自动划分
一个例子：A 向 B 转账 500元，过程如下：
1. 检查 A 的账户余额，
2. A 账户扣除 500元
3. B 账户加 500元

事务的特性：ACID

原子性(Atomicity)：整个事务是原子、不可分的。一个事务的所有操作要么全部commit成功，要么失败全部rollback。对于一个事务来说，不可能只执行其中的一部分SQL。
- 例子：A 向 B 转账 500元，分为两步：1）A 账户扣款 500元，2）B 账户加款 500元。如果两步之间发生故障，那么A和B的余额都恢复到原始状态。
一致性(Consistency)：数据库总是从一个一致性的状态转换到另外一个一致性的状态。事务不能破坏数据库的约束条件，例如主键、外键、用户自定义CHECK（如，余额不能为负）。
隔离性(Isolation)：并发执行的多个事务之间相互隔离。一个事务在提交以前，对数据库的修改对其他事务不可见。
持久性(Durability)：一旦事务提交，则其所做的修改就会永久保存到数据库中。此时即使系统崩溃，修改的数据也不会丢失。

一段关于事务的 C语言代码

#include <stdio.h>
#include "prompt.h"

// sqlca 是错误处理所用的区域
EXEC SQL include sqlca;

char cid_prompt[ ] = "Please enter customer id:	";
int main(){

    // 定义变量
    EXEC SQL BEGIN DECLARE SECTION;
        char cust_id[5], cust_name[14];
        float cust_discnt;
        char user_name[20],user_pwd[20];
    EXEC SQL END DECLARE SECTION;
    
    // SQL 错误捕获语句
    EXEC SQL whenever sqlerror goto report_error;
    EXEC SQL whenever not found goto notfound;
    
    // 连接数据库
    strcpy(user_name, "poneilsql");
    strcpy(user_pwd, "XXXX");
    EXEC SQL connect :user_name	identified by :user_pwd;
    
    // 主要逻辑
    while((prompt(cid_prompt,1,cust_id,4)) >=0) {
        EXEC SQL select cname,discnt
            into :cust_name, :cust_discnt
            from customers where cid=:cust_id;
        EXEC SQL commit work;
        printf("Customer’s name is %s and discount is %5.1f\n", cust_name, cust_discnt);
        continue;
    }

    // 定义这些错误
    notfound:
        printf("Can’t find customer %s, continuing\n", cust_id);
        EXEC SQL commit release;
        return 0;
    
    report_error:
        // 如果这里也有 SQL 语句，并且这个 SQL 语句可能报错，
        // 那么要用 EXEC SQL whenever sqlerror continue; 覆盖掉，否则会陷入死循环
        print_dberror();
        EXEC SQL rollback release;
        return 1;
}

游标

游标（Cursor）的原因：SQL 返回结果是单行时可以直接传给C语言的变量，但是如果返回多行结果，则需要使用 Cursor

Cursor 是指向记录的指针
指针移动，指向一行。一行一行处理，最后关闭。

// 定义一个 cursor 并命名为 cursor_student
EXEC SQL DECLARE cursor_student CURSOR FOR
SELECT id, name, class FROM table_student WHERE class = '101';

// 打开 cursor
EXEC SQL open cursor_student;

// 取出一条数据，将其内容放入变量中
EXEC SQL FRTCH cursor_student INTO :v_id, :v_name, :v_class;
...


// 关闭 cursor
EXEC SQL CLOSE cursor_student;

说明

cursor 可以多次打开/关闭
cursor 只能从上到下移动。大多数 DBMS 不支持 cursor 向上移动（支持的叫做 可滚动游标），只能再次访问需要关闭后重新打开。
可以通过 ODBC（Open DataBase Connectivity）通用接口支持可滚动游标

数据的删、改、插

两种方法：1）使用 SQL 语句，2）使用 cursor

// 使用 sql 语句删除
EXEC DELETE FROM tabltable_student WHERE ...;

// 使用 sql 更新
EXEC SQL UPDATE tabltable_student SET ...;

// 使用 sql 插入
EXEC SQL INSERT INTO tabltable_student(id, name, class) ...;

// 使用 cursor 删除/更新
EXEC SQL DECLARE cursor_student CURSOR FOR
SELECT id, name, class from table_student WHERE class = '101'
FOR UPDATE OF class // FOR UPDATE: 删除/更新；FOR READ ONLY
;

EXEC SQL OPEN cursor_student; // 实际执行 SQL 是在 OPEN 阶段进行的
while(1){
    EXEC SQL FETCH cursor_student INTO :cust_id;
    if(rand()>0.3){
        // 删除
        EXEC SQL DELETE FROM table_student WHERE CURRENT OF cursor_student;
    }else{
        // 更新
        EXEC SQL UPDATE SET class='102' WHERE CURRENT OF cursor_student;
    }
}

EXEC SQL CLOSE cursor_student;

动态SQL

动态 SQL 是用程序构造整个 SQL 语句（字符串类型），然后让数据库执行它。

// 静态 SQL：SQL 语句中的程序已经写好了，只需要把参数用变量传给 SQL 语句
name1 = '张三';
EXEC SQL SELECT id, name, class into :v_id, :v_name, :v_class FROM table_student 
WHERE class = '101' AND name = :name1; // 把参数用变量传给 SQL 语句

// 或者用游标（前面详细解释过了）


// 动态 SQL
// 省略：include 和变量声明
EXEC SQL INCLUDE sqlca;

EXEC SQL BEGIN DECLARE SECTION;
    char user_name[] = "Scott";
    char user_pwd[] = "pwd";
    // 用法1: 动态构造的 SQL 语句，然后立即执行
    char sqltext1[] = "DELETE FROM table_customer WHERE cid = \'c006\'";

    // 用法2：先编译，后传入参数
    char sqltext2[] = "DELETE FROM table_customer WHERE cid = :dcid";

EXEC SQL END DECLARE SECTIOIN;

int main(){
    EXEC SQL WHENEVER sqlerror goto report_error;
    EXEC SQL connect :user_name identified by :user_pwd;
    
    // 用法1: 立即执行动态 SQL
    EXEC SQL EXECUTE IMMEDIATE :sqltext1;

    // 用法2: 先编译再执行
    EXEC SQL PREPARE sql_tmp FROM :sqltext2; // 编译
    int cust_id = 1003;
    EXEC SQL PREPARE sql_tmp USING :cust_id; // 用 cust_id 替换 dcid，并执行

    exec sql commit release;
    return 0;
    
    report_error: // 错误处理
        ...
}

其它知识

数据字典：存放数据库和表的元数据，例如：

关系的名字、属性名、数据类型、视图、完整性约束
用户的账户、密码
统计与描述性数据
物理文件组织信息
索引相关信息

可以用 SQL 语句来查这些信息，例如：SELECT Table_Name FROM Tables WHERE ...

SQLDA: 是一个 struct，描述动态 SQL 语句参数和查询结果信息。例如查询结果有多少列、数据类型、长度等

ODBC（Open DataBase Connection）：不同语言与不同数据库之间通讯的标准。

JDBC（Java DataBase Connection）：ODBC 的 Java 版本。

JDBC使用步骤

传递一个 Driver 给 Driver Manager，加载数据库驱动；
通过 URL 的到一个 Connection 对象，建立数据库连接；
创建 Statement 对象，用来查询、修改数据
执行查询，并返回一个 ResultSet，提取数据到应用程序

函数依赖

关系依赖: 设 $R(U)$ 是 $U = \{ A_1, A_2,..., A_n \}$ 上的一个关系模式，$X,Y \subseteq U$，如果 $R$ 上的任意关系 r，r 中不可能有两个元组满足在 $X$ 中的属性值相等，而在 $Y$ 中的属性值不等，则称 “X函数决定Y” 或 “Y函数依赖于X”，记做 $X \to Y$

用文字描述是：X（一个属性的集合）的一行数据，可以唯一确定 Y（另一个属性集合）的值

用实际例子描述：假设 R(学号, 姓名, 年龄, 班号, 班长, 课号, 成绩)，那么：

{学号} → {姓名, 年龄}
{班号} → {班长}
{学号, 课号} → {成绩}

一些相关的定义

$X \to Y$ 并且 $Y \not\subset X$，那么称 $X \to Y$ 是 非平凡的函数依赖
若 $X \to Y$ 并且 $Y \to X$，记做 $X \leftrightarrow Y$
依赖的否定，记做 $X \not \to Y$
$X \to Y$ 有两种理解：1）基于模式 R，则要求任意可能的 r 都成立。2）基于某个具体的关系 r，对其成立即可。
- 基于 r 的某个属性集 $X$，如果 r 中没有相同的两个元组存在，那么 $X \to Y$ 对任意 $Y$ 都成立

一些结论：

如果 $X \to Y$，那么如果 X 上的值相同，那么 Y 上的值必然相同。

部分函数依赖、完全函数依赖: $R(U)$ 中，如果 $X \to Y$，并且对于 $X$ 上任意真子集 $X'$ 都有 $X' \not\to Y$ 则称为 $Y$ 完全函数依赖 于 $X$，记做 $X \xrightarrow{f} Y$，否则称为 $Y$ 部分函数依赖 于 $X$，记做 $X \xrightarrow{p} Y$

实际例子：假设 U(学号, 姓名, 年龄, 班号, 班长, 课号, 成绩)，那么：

{学号, 课号} $\xrightarrow{f}$ U
{学号, 课号} $\xrightarrow{p}$ {姓名}
{学号, 课号} $\xrightarrow{f}$ {姓名}

部分函数依赖，说明存在非受控冗余。

传递函数依赖: $R(U)$ 中，如果 $X \to Y, Y \not\subset X$（也就是非平凡的函数依赖），且 $Y \to Z, Z \not\subset Y$（也是非平凡函数依赖），且 $ Z \not\subset X, Y \not\to X$，则称 Z 传递函数依赖 于 X

实际例子：假设 U(学号, 姓名, 年龄, 班号, 班长, 课号, 成绩)，那么：

{学号} → {班号}; {班号} → {班长}
{学号} → {班长} 是一个传递依赖

传递函数依赖，说明存在非受控冗余。

几个相关概念

候选键: K 是 $R(U)$ 的属性组合，如果 $K \xrightarrow{f} U$，则称 $K$ 是 $R(U)$ 上的 候选键（Candidate Key）

一些说明：

如果有多个候选键，可选任意一个做为主键（Primary Key）
候选键中的属性称为 主属性（Prime Attribute），其它是 非主属性
如果 K 是 R 的一个候选键，$K \subset S$，称 S 是 R 的一个超键（Super Key）

外键

X 是 $R(U)$ 的属性组合，X 不是 R 的候选键，但是另一个关系的候选键，称它为外键（Foreign Key）

逻辑蕴含

F 是 $R(U)$ 的一个函数依赖集合，$X,Y \subseteq R$，如果 F 中的函数依赖能推导出 $X \to Y$，称 F 逻辑蕴含 $X \to Y$，或者 $X \to Y$ 是 F 的逻辑蕴含，记做 $F \models X \to Y$

这里的推导，指的是使用 Armstrong 公理和推论的推导

闭包

被 F 逻辑蕴含的所有函数依赖集合称为 F 的闭包（Closure），记做 $F^{+}$

语言描述解释：F 是一个集合，里面是 n个函数依赖，由这 n个函数依赖推导出的所有函数依赖，其集合为 $F^+$
若 $F^+ = F$ 则称 F 是一个 全函数依赖族（函数依赖完备集）

Armstrong公理，设 F 是 $R(U)$ 的一组函数依赖，则：

自反律 (Reflexivity rule) 若 $Y \subseteq X \subseteq U$，则 $X \to Y$ 被 F 逻辑蕴含
增广律 (Augmentation rule) 若 $X \to Y \in F$，且 $Z \subseteq U$，则 $XZ \to YZ$ 被 F 逻辑蕴含
- 其中的 $XZ$ 是两个属性集的并
传递律 (Transtivity rule) 若 $X \to Y \in F$，且 $Y \to Z$，则 $X \to Z$ 被 F 逻辑蕴含

定理

合并律 (Union Rule)：若 $X \to Y, X \to Z$, 则$X \to YZ$
伪传递律 (Pseudo Transitivity)：若 $X \to Y, WY \to Z$, 则 $XW \to Z$。
分解律(Decomposition Rule)：若 X→Y且Z⊆Y, 则X→Z。
如果 $A_1, A_2, …, A_n$ 是属性，那么 $X \to \{ A_1, A_2, ..., A_n \}$ 当且仅当 $\forall i, X \to A_i$

属性集的闭包

对于 $R(U)$，其中 $U = \{ A_1, A_2,..., A_n\}$，$X \subseteq U$ 的 属性集闭包 是 $X^+_F = \{ A_i \mid F \models X \to A_i \}$

与前面的 F 的闭包不一样

定理

$F \models X \to Y$ 当且仅当 $Y \subseteq X^+_F$
Armstrong公理是有效的（其所有的推导是正确的）、完备的（所有的推导都可以从公理推导出来）

求属性集闭包的算法

输入：R(U)，以及函数依赖集合 F，求 X 的属性集闭包
算法：
1. 令 $X^{(0)} = X$
2. 遍历 F，使满足的属性集合加入临时集合 $B$
3. $X^{(i+1)} = X^{(i)} \cup B$
4. 如果 $X^{(i+1)} = X^{(i)}$ 则算法终止，否则回到2
输出：$X^+_F = X^{(i+1)}$

覆盖(Cover): $R(U)$ 上的两个函数依赖集合 F, G，如果 $F^+ = G^+$，称为 F 和 G 等价，或者 F覆盖G，或者 G覆盖F

定理

$F^+ = G^+ $ 当且仅当 $F \subseteq G^+ \land G \subseteq F^+$

定理：每个函数依赖集 F，都可被一个“右端至多一个的函数依赖”的集合覆盖。

证明思路，对于 $X \to Y \in F$，其中 $Y = A_1 A_2…A_k$，那么拆分为 $X\to A_1, X \to A_2,…, X \to A_k$ 之后，它们也是等价的

最小覆盖

若 F 满足以下条件，则称F为 最小覆盖(minimal Cover)或 最小依赖集 (minimal set of Functional Depandency)：

F中每个函数依赖的右部是单个属性；
对任何 $X \to A \in F$, 有$F− \{ X \to A \}$ 不等价于F；
对任何$X \to A \in F, Z \subset X$，$(F− \{ X \to A \}) \cup \{ Z \to A \}$ 不等价于F。

定理：每个函数依赖集F都有等价的最小覆盖F'。

【证明兼算法】：

由（前面的）定理（每个函数依赖集 F，都可被一个“右端至多一个的函数依赖”的集合覆盖），对所有的函数依赖拆分得到一个 G，它与 F 等价
对 G 中的每个依赖，检查 $G - \{ X \to Y\}$，若其等价于 G，则剔除。最终得到 G'
对 G' 中每个依赖，检查其是否可以消去左侧属性，如果消去后仍然保持等价，则消去。最终得到 F'
F' 就是等价的最小覆盖

关系范式

第一范式（1NF）、第二范式（2NF）、第三范式（3NF）、第四范式（4NF），是越来越严格的

1NF: 若关系模式R(U)中关系的每个分量都是不可分的数据项(值、原子)，则称R(U)属于第一范式，记为：$R(U) \in 1NF$

caption: 第一范式

非 1NF 转换为 1NF 的方法

拆分，例如，把字段 name拆分为两个字段 Iname 和 Fname
面向对象，name 数据类型为对象 struct name(Iname, Fname)

2NF

$R(U) \in 1NF$ 且U中的每一 非主属性 完全函数依赖于 候选键，则称R(U)属于第二范式，记为：$R(U) \in 2NF$

例子：R(学号, 姓名, 课程号, 课程名, 分数)
候选键为 {学号, 课程号}，非主属性是 姓名, 课程名, 分数
检查每个 “候选键 → 非主属性”，发现 {学号, 课程号} → {姓名} 不是完全函数依赖，因为可以去掉一个 {学号} → {姓名}；同理 {学号, 课程号} → {姓名} 也不是完全函数依赖

非 2NF 转换为 2NF的方法：拆分为多个表：学生(学号, 姓名)，课程(课程号，课程名)，选课(学号, 课程号, 成绩)

3NF

若 $R(U，F) \in 2NF$ 且 R中不存在这样的情况：候选键X，属性组 $Y \subseteq U$和非主属性A, 且 $A \not\in X, A \not\in Y, Y\not\subset X, Y \not\to X$，使得 $X \to Y，Y \to A$成立。满足以上条件则称R(U)属于第三范式，记为：$R(U) \in 3NF$

简单地说，不存在：非主属性“通过另一个非主属性”间接依赖于候选键的情况
举例（前面举过了）R(学号, 姓名, 年龄, 班号, 班长)，不符合 3NF
- {学号} → {班号}; {班号} → {班长}
- {学号} → {班长} 是一个传递依赖
- 解决方法：拆分为多个表：R1(学号, 姓名, 年龄, 班号)，R2(班号, 班长)

BCNF(Boyce-Codd)范式

若 $R(U，F) \in 1NF$, 若对于任何 $X \to Y \in F$ (或 $X \to A \in F$), 当 $Y \not\subset X$ (或 $A\not\in X$)时， X必含有候选键，则称R(U)属于 Boyce-Codd范式，记为：$R(U) \in BCNF$

描述：每一个依赖，都依赖候选键
举例： 邮编(城市, 街道, 邮政编码)
- 函数依赖 {城市, 街道} -> 邮政编码,邮政编码 -> 街道
- 候选键是 {城市, 街道}
- 邮政编码 -> 街道 不含候选键，因此不满足 BCNF 范式
- 它满足 3NF

定理：如果 $R(U) \in BCNF$，那么 $R(U) \in 3NF$

模式分解: 把关系 R(U) 分解为一组等价的子集 $\{ R_1(U_1), R_2(U_2), ..., R_k(U_k)\}$

模式分解需要关注：

分解后数据内容方面是否等价：分解的无损连接性
分解后在数据依赖方面是否等价：分解的保持依赖性

数据库物理存储

两个基本问题：

如何高效率存储？数据组织与索引
如何快速查询？查询实现与查询优化

三种文件组织方法

堆文件、顺序文件、散列文件

【基础知识回顾】

操作系统-文件系统

逻辑 -> 物理对应关系，对于操作系统是文件 -> 磁盘块，对于 DMS 是表 -> 磁盘块

数据库在磁盘上的存储

定长记录 vs 变长记录
记录不跨磁盘块 vs 记录跨磁盘块
- 记录跨磁盘块可以解决空间，但是需要指针指向下一个磁盘块
磁盘块的分配
- 连续分配。速度快，扩展困难
- 链接分配。使用指针指向下一个数据块
- 按 Segment 分配。Segment 内部连续分配，Segment 之间链接分配
- 索引分配。索引块中存放指向数据块的指针。相当于 DMS 做了一个 “文件分配表”

文件组织

文件组织1: 无序记录文件 heap 或 pile file

记录的存储顺序是无序的
更新效率高、检索效率低
新插入的记录，两种方式：
1. 插入到末尾
  - 定时做数据库重组（Reorganization），回收闲置空间
2. 插入到空洞

文件组织2: 有序记录文件

检索效率高（仅限于用排序字段检索时），更新效率很低
一些优化
- 新插入的记录，放入临时区；定时做做数据库重组（Reorganization）

文件组织3:散列文件

按照某属性（或者属性组），依据散列函数分桶
检索和更新效率都高
桶满时：
- 链接法，新记录放入“溢出区”，用指针指向它。
- 其他方法，如动态散列技术

文件组织4:聚簇文件（Clustering file）

单表：相同或相似属性值的记录存放在连续的磁盘中
多表：几个相关的表，存放在一个文件中。可以提高多表查询速度

文件组织

文件组织2

Oracle 可以通过 SQL 语句，指定文件组织的参数（语句不写了）

索引技术

索引是帮助快速查询的一种设计

排序索引
散列索引

索引文件小很多，因此可以全量放入内存，因此可以极大提高速度。

衡量索引设计的好坏

访问时间
插入时间
删除时间
增加的空间使用
存取有效性。
- 支持单一值
- 支持返回值
一致性：索引和数据要同步更新

稠密索引（undense index） vs 稀疏索引（sparse index）

稠密索引：所有记录都被索引
- 几种情况：
- 索引是候选键的（前面有候选键的定义，候选键唯一）：直接通过索引查找记录
- 索引不是候选键，主文件按索引字段排序，索引去重
- 索引不是候选键，主文件不按索引字段排序，索引不去重
- 索引不是候选键，主文件不按索引字段排序，索引指向桶
稀疏索引：只有一部分记录被索引
- 要求：主文件按索引字段排序存储
- 查找算法：使用稀疏索引确定范围，然后遍历这个范围
- 评价：索引占用的空间少，维护任务更轻，但查找速度更慢
平衡：索引的指针不是指向记录，而是指向一个磁盘块

主索引 vs 辅助索引

主索引：每个存储块，有一个索引项
- 主索引对应的字段（记为k），主文件按 k 排序存储
- 主索引是稀疏索引
辅助索引
- 对应：非排序字段
- 如果字段值不唯一，用链表保存所有位置
- 辅助索引是稠密索引
比较
- 一个主文件，最多可以有一个主索引，多个辅助索引
- 主索引通常在主码/排序码上，辅助索引在其他属性上
- 辅助索引上的查询快很多

聚簇索引 vs 非聚簇索引

聚簇索引：索引中临近的记录，在主文件中也是临近存储的
非聚簇索引：索引中临近的记录，在主文件中不一定是临近存储的
比较
- 一个主文件只能有一个聚簇索引，但可以有多个非聚簇索引
- 主索引通常是聚簇索引，辅助索引通常是非聚簇索引

倒排索引：一种针对文档检索的索引

正排索引，文档1 -> 词1, 词2, …
倒排索引，词1 -> 文档1, 文档9, …

多级索引：索引比较大，无法一次性读入内存，设计多级索引

B树/ B+树

多属性索引：多个字段组合起来组成的索引

散列索引：引入 Hash 技术组成的索引

网格索引：多个索引字段做交叉定位检索

Btree

B+树可用于：

键、稠密索引
- 主文件不必按 key 排序
- 指针指向记录
键、稀疏索引
- 主文件必须按 key 排序
- 指针指向数据块
B+树用于非键、稠密索引，索引不重复
- 主文件必须按 key 排序
- 指针指向记录
B+树用于非键、稠密索引，索引重复
- 主文件不必按 key 排序
- 指针指向记录

散列索引

使用 Hash 技术
指向桶
如果主桶溢出，用链表指向一个下一个新桶
如果桶的数目是固定的：静态散列索引。如果桶的个数是动态的：动态散列索引

动态散列索引

原因：静态散列索引，当数据量增加时，可能需要用链表指向下一个新桶，这样查询效率就低了
思路：假设 Hash 函数的值为 m 位（例如 128位二进制），当前只用前 k 位做分桶，当一个桶不够用时，使用前 k+1 位做分桶（相当于桶分裂为2个）
极端情况：某2个值的 Hash 值前 n位都一样，某个桶一直分裂，最终不得不使用 n 位散列值，以及 $2^n$ 个桶，尽管只有2条数据。解决方法：线性散列索引

线性散列索引

允许溢出，溢出先用链表管理
每次达到最大容量的70%时，桶分裂
每次分裂增加一个桶
（不细写了）

数据库查询

查询的实现与查询优化
SQL 语句 => 关系代数 => 优化后的关系代数 => 每个运算，选择执行程序，形成查询计划 => 按计划执行，并返回结果

每种关系代数，如何转化为程序执行呢？

归类数据库的三大类操作

一次单一元组的一元操作
- 选择、投影
- 迭代器算法
整个关系的一元操作
- Distinct, Group by, Sorting
- 一趟扫描算法，两趟扫描算法，多趟扫描算法
整个关系的二元操作
- 集合运算，并、交、差
- 积、连接

theta-连接（$R \mathop{\bowtie}\limits_{A \theta B} S$）的算法实现：暴力遍历（第一个版本）

for i in A: for j in B: if condition: collect
性能灾难，尤其是要按磁盘块装载到内存
不同的物理实现：
- 3个内存页：A，B，结果，各对应一个内存页
- 全放入内存（内存充分大）：A，B，结果，都放入内存，做遍历
- 半内存。A可以全量放入内存，B不能。B分配 k 个内存页
- 如果都不能放入内存。假设内存页为 M 个，给 A 分配 M-2个，B分配1个，结果分配1个。
- 还有很多算法：归并排序、散列连接、索引连接算法

迭代器算法

对于多步的选择、投影，有两个策略

物化计算策略
- 按步骤计算，每一步计算结果放入到 temp_i
- 每个中间结果都存储（内存或磁盘）
流水线计算策略

迭代器-流水线策略

流水线策略用面向对象方式实现就比较容易

// 迭代器抽象类
class Iterator{
    Void Open();
    tuple GetNext(); 
    void Close();
    ...
}

UNION 操作对应的迭代器（伪代码）

Open(){
    R.Open();
    cur = R;
}


GetNext(){
    if (cur == R){
        t=R.GetNext();
        if(t != null) {return t}; // 获取下一个
        else {
            // R 已经处理完了
            S.open()
            cur = S
            };
    }
    return S.GetNext()
}

Close(){
    R.Close();
    S.close();
}

SELECTIOIN 操作（就是 where 语句）对应的迭代器

Open(){R.Open();}
GetNext(){
    while True{
        t = R.GetNext()
        if t is null: return; // 迭代到末尾了
        if(condition){
            return t
        }
    }
}
Close(){R.Close();}

投影操作

Open(){
    S.Open();
}
GetNext(){
    t = S.GetNext()
    if (t != null){
        p = projection(t, *args);
        return p;
    }
    else return null;
}
Close(){
    S.close()
}

以上投影操作的 S = SELECTION ，即可实现选择+投影的流水线操作

一趟扫描算法

Distinct 操作

distinct

Group By 操作

groupby

集合运算：并、交、差，类似（不重复画了）

theta-连接操作 （第二个版本）：

join

theta-连接操作 （第三个版本）：

R 表和 S 表都在连接属性 Y 上建立B+Tree
使用 Zig-Zag 连接算法，O(m+n) 复杂度

join

多趟扫描算法

问题：

Distinct, Group BY, Order By 理论上需要任何一个元组与所有元组比较，才能确定是否重复
如果这些待处理数据量远大于可用的内存怎么办？
例如：只有8块内存，如何排序 70块数据集？如何对70块数据集做去重？如何分组？

两趟扫描算法的思路

第一趟划分子集，使其满足某种特性
第二趟处理每个子集
合理设计两趟算法，使得第二趟在每个子集处理完毕，就等同于在全集上处理完毕

2_stage

两阶段多路归并排序（TPMMS，Two-Phase Multiway Merge-Sort）

外排序问题：待排序的数据无法全部放入内存
举例：可用内存6块，每块可装载5个元素，待排序数据60个元素。如何排序？
60个元素分为 12 个序列，每个序列有5个元素。最多可以5路（这里用4路演示）

TPMMS

算法步骤

第一步。每个序列内部排序
第二步。使用n趟扫描算法

第 1 趟

run_1  ┐
run_2  │
...    ├── 4路归并 ──> new_run_1
run_4 ┘

run_5 ┐
...    ├── 4路归并 ──> new_run_2
run_8 ┘

run_9 ┐
...    ├── 4路归并 ──> new_run_2
run_12 ┘

第一趟结束后，获得 3 个更大的有序段

第 2 趟

new_run_1
new_run_2
new_run_3
      ↓
4路归并
      ↓
最终有序文件

归并所需要的趟数是 $\log_k r$

初始 r 个有序段
每次 k 路归并
上面的例子是 $\log_4 {12} $（2趟）

其它细节

多路归并时，需要不断的：弹出当前最小数，插入新数。这一步有很多算法：
- 暴力遍历
- 最小堆
- 胜者树
- 败者树

多趟算法还可以用于：

group by
去重（需要去重的 UNION、交运算等）
- 也是先对每个序列排序，然后 n趟扫描

theta-连接操作 （第四个版本）：

分片，每个分片内排序
n 趟扫描
- 归并时区分是 R 的输入还是 S 的输入，以此得出结果

基于散列的两趟扫描算法

第一趟：用 Hash1，散列到 M-1 个分片
第二趟：处理每个子表，用 Hash2 将其散列

基于散列的两趟扫描算法：Distinct, Group By

基于散列的两趟扫描算法：

集合运算：交、并、差
theta-连接操作（第五个版本）

数据库查询优化

为什么？举例：

学生表 Student（10000条），课程表Course（1000条），选课表（100000*50，每位学生50门课程）
3个表 JOIN，笛卡尔有 5e12 条记录
发现改变关系代数的操作次序，可以极大提高效率

数据库查询优化的层面

语义优化。优化 SQL 语句，例如去掉实际上没用到的表。
逻辑查询优化。优化的是操作执行顺序。
物理查询优化。优化的是存取、算法选择、执行次序。

逻辑查询优化

语法优化 基于关系代数的一系列等价定理

定理L1：连接与连接，积与积的交换律
设 $E_1, E_2$是关系代数表达式， $F$是 $E1, E2$ 中属性的附加限制条件，则有：

$E_1 \mathop{\bowtie}\limits_{F} E_2 = E_2 \mathop{\bowtie}\limits_{F} E_1$
$E_1 \mathop{\bowtie} E_2 = E_2 \mathop{\bowtie} E_1$
$E_1 \times E_2 = E_2 \times E_1$
并运算、交运算，也满足交换律

作用：通常把集合小的表达式，先装入内存

定理L2： 连接与连接、积和积的结合律
若 $E_1, E_2, E_3$ 是关系代数表达式，$F_1，F_2$ 是条件，则有：

$(E_1 \mathop{\bowtie}\limits_{F_1} E_2) \mathop{\bowtie}\limits_{F_2} E_3 = E_1 \mathop{\bowtie}\limits_{F_1} (E_2 \mathop{\bowtie}\limits_{F_2} E_3)$
$(E_1 \mathop{\bowtie} E_2) \mathop{\bowtie} E_3 = E_1 \mathop{\bowtie} (E_2 \mathop{\bowtie} E_3)$
$(E_1 \times E_2) \times E_3 = E_1 \times (E_2 \times E_3)$

作用：优先计算集合小的表达式

定理L3：投影串接律
设属性集 $\{A_1, ... , A_n\} \subseteq \{ B_1, ... ,B_m \}$, E是表达式，则有：

$\pi_{A_1, …, A_n} (\pi_{B_1, …, B_n}(E)) = \pi_{A_1,…, A_n}(E)$

作用

两遍扫描变成一遍扫描
可以反向使用，做属性扩展，便于之后的移动操作

定理L4：选择串接律
若E是关系代数表达式，F1, F2是条件，则有：

$\sigma_{F_1} (\sigma_{F_2} (E)) = \sigma_{F_1 \land F_2} (E)$

作用

两遍扫描变成一遍扫描
可以反向使用，分解复杂操作，便于之后的移动操作

定理L5：选择和投影交换律
设条件 F 只涉及属性 ${A_1, …, A_n}$， E 是关系表达式，则有：

$\pi_{A_1, … , A_n} (\sigma_F(E)) = \sigma_F(\pi_{A_1,…,A_n}(E))$

定理L6：选择与笛卡尔积的交换律
设 $E_1, E_2$ 是关系代数表达式

若条件 $F$ 只涉及 $E_1$ 中的属性，则有：
- $\sigma_F(E_1 \times E_2) = \sigma_F(E_1) \times E_2$
若 $F = F_1 \land F_2$，其中 $F_1, F_2$ 分别只涉及 $E_1, E_2$ 中的属性，则有：
- $\sigma_F(E_1 \times E_2) = \sigma_{F_1}(E_1) \times \sigma_{F_2}(E_2) $
若 $F = F_1 \land F_2$，其中 $F_1$ 只涉及 $E_1$ 中的属性，而 $F_2$ 同时涉及 $E_1, E_2$ 中的属性，则有：
- $\sigma_F(E_1 \times E_2) = \sigma_{F_2}\left(\sigma_{F_1}(E_1) \times E_2\right)$

作用：

选择操作 下推的核心依据。

定理L7：投影与笛卡尔积的交换律
设 $E_1, E_2$ 为关系代数表达式，${A_1,\ldots,A_n}$ 是出现在 $E_1$ 或 $E_2$ 中的一组属性。这组属性可以划分为两个部分：${B_1,\ldots,B_m}$ 是属于 $E_1$ 的属性，${C_1,\ldots,C_k}$ 是属于 $E_2$ 的属性，则有：

$\pi_{A_1,\ldots,A_n}(E_1\times E_2)=\pi_{B_1,\ldots,B_m}(E_1)\times\pi_{C_1,\ldots,C_k}(E_2)$

作用：

投影操作 下推的核心依据。

定理L8：选择与并的交换律
设 $E_1, E_2$ 是关系代数表达式，$F$ 是条件，则有：

$\sigma_F(E_1 \cup E_2) = \sigma_F(E_1) \cup \sigma_F(E_2)$
注意：该定理要求 $E_1, E_2$ 并相容。

作用：

降低中间结果

定理L9：选择与差的交换律
设 $E_1, E_2$ 是关系代数表达式，$F$ 是条件，则有：

$\sigma_F(E_1 - E_2) = \sigma_F(E_1) - \sigma_F(E_2)$

作用：

降低中间结果

定理L10：投影与并的交换律
设 $E_1, E_2$ 是关系代数表达式，${A_1,\ldots,A_n}$ 是 $E_1, E_2$ 中的一组属性，则有：

$\pi_{A_1,\ldots,A_n}(E_1 \cup E_2) = \pi_{A_1,\ldots,A_n}(E_1) \cup \pi_{A_1,\ldots,A_n}(E_2)$

但是：

投影、差集运算没有这个定理

基于代数定理的语法优化算法

根据定理 L4，把选择表达式变成串接形式
对每个选择，根据定理 L4 至 L9，尽可能把它移到树的底部
对每个投影，根据定理 L3, L7, L5, L10，尽可能把它移动到树的底部
根据定理 L4, L5 把串接的选择和投影组合为单个选择、单个投影，或者一选择后跟一投影
对修改后的语法树分组：
- 每个二元运算结点(积、并、差、连接等)和其所有一元运算直接祖先结点放在一组；对于其后代结点，若后代结点是一串一元运算且以树叶为终点，则将这些一元运算结点放在该组中；若该二元运算结点是笛卡儿积，且其后代结点不能和它组合成等连接，则不能将后代结点归入该组。
产生一个程序，以每组为一步，后代组先执行。

以SQL为例：

-- 查询 20260712 之前所有被借出的书名
SELECT Title FROM
(
    SELECT * FROM LOANS, BORROWERS, BOOKS
    WHERE BORROWERS.CARD_NO = LOANS.CARD_NO
    AND BOOKS.LC_NO = LOOANS.LC_NO
)
WHERE Date <= '20260712'

第一步 改为串接

修改前: $\sigma_{F_1 \land F_2 \land …, \land F_n}(E)$
修改后: $\sigma_{F_1} (\sigma_{F_2}(…(\sigma_{F_n}(E))))$

逻辑查询优化

物理查询优化

获取关系元组的操作

暴力扫描

物理查询优化的关键：代价估算

I/O 访问次数
CPU占用时间
内存代价
中间结果存储代价
算法计算量
网络通信量

代价估算的依据，是统计信息（存放在数据字典或系统目录中）

T(R): 关系 R 的元组数目
B(R): 关系 R 的磁盘块数目
I(R): 关系 R 的单个元组字节数
f(R): 一个块能存储的 R 的元组数目
V(R,A): R 中属性 A 的去重数目
SV(R,A): R 中属性 A 平均每个取值的数目
每个磁盘块的字节数
….

以上信息需要 DBA 使用特定命令完成。因此性能下降后，需要 DBA 运维。（命令就不写了）

代价估算的一些例子

一个投影 $\pi_L(R)$ 的大小

行数没变是 T(R)
但可能减少了每个元组的的大小
根据行数、新元组大小、磁盘块大小，可以估算用到的磁盘块

一个选择 $\sigma_{A=c}(R)$

按照平均分布来估算 1/V(R,A)
或者直接按照总量的 1/10 估算
或者按照总量估算

一个选择 $\sigma_{A<c}(R)$ 的估算

按照一半估算
按照总量估算
按照 1/3 估算（实际操作较准）

一个选择 $\sigma_{A<\not= c}(R)$ 的估算

按照平均分布来估算 1 - 1/V(R,A)
按照 1- 1/10 估算

复杂条件选择：拆开各自估算，然后用概率合算

$\sigma_{A<10 \, \mathrm{AND} \, B=20}(R)$：拆开后概率相乘
$\sigma_{A<10 \, \mathrm{OR} \, B=20}(R)$：拆开后按逻辑或合算

自然连接 $R \bowtie_A S$

假如 V(R,A) >= V(S,A)，值相等的概率为 1/V(R,A)
反之亦然
因此概率为 1 / max(V(R,A), V(S,A))
因此 T = T(R) T(S) / max(V(R,A), V(S,A))

并发控制

为什么需要并发控制

caption: 并发中的一些不一致现象

并发中的一些不一致现象：

丢失更新（Lost Update）：两个事务同时读一个值，分别修改后写回。导致一个修改被另一个覆盖
不可重复读（Non-repeatable Read）：同一个事务，对同一个值读2次
- 什么会有读2次的需求？一个事务可能有多个子模块，每个子模块要根据 A 字段记录的状态做不同的行为。
- 例如，某个事务要处理订单+支付+结算，每个子模块都要读一次订单状态。如果另一个事务把订单状态设定为 Canceled，就会产生混乱
脏读（Dirty Read）：一个事务读取了另一个事务尚未提交的数据，但后者回滚，导致读取的数据是无效的
幻读
- 例子: 计算平均工资时，先计算 SUM(A)，再计算 COUNT(A)，执行过程中，另一个事务 UPDATE 插入一条数据，那么计算的值不对应任何时刻的真实值

事务（Transaction）前面解释过。

一个或多个 SQL 组成的
结束前有提交与撤销
每次 commit/rollback，都产生一个事务（即使是循环中执行）
事务的特性：ACID（前面解释过）

事务调度：n个并行的事务的子任务（读、写、提交、回滚）的执行顺序

可串行性：某个并发调度的执行结果，与某个串行调度的执行结果等价。

冲突：某两个动作，如果他们交换顺序，那么会改变至少一个事务的行为。

有冲突的两个操作是不能交换顺序的，没有冲突的两个事务是可以交换顺序的
同一事务的任何两个操作都是冲突的
不同事务对同一元素的写操作是冲突的
不同事务对同一元素的一读一写是冲突的
冲突可串行性：某个调度，交换相邻两个无冲突的操作，最后可以转换到一个串行调度。

冲突可串行性是严格的情况：

并发调度的正确性 $\supseteq$ 可串行性 $\supseteq$ 冲突可穿行性
因此用冲突可串行性来判断调度的正确性（充分非必要条件）

冲突可串行性的判别算法

构造一个有向图，其节点是事务
如果 T_j 的某个操作，和 T_k 的某个操作发生冲突，则添加边 T_i -> T_j
- 两次遍历 O(n^2)
判断此有向图是否有环，如果没有环，则是冲突可串行化的

# 冲突可串行（图左）
r2(A); r1(B); w2(A); r3(A); w1(B); w3(A); r2(B); w2(B)

# 非冲突可串行（图右）
r2(A); r1(B); w2(A); r2(B); r3(A); w1(B); w3(A); w2(B)

caption: 冲突可串行/非冲突可串行

基于锁的并发控制

分类

基于锁的并发控制
基于时间戳+回滚的并发控制
基于有效性确认+回滚的并发控制

基于锁的并发控制

新增两个操作:
L_i(A) 事务 T_i 对数据 A 加锁
U_i(A) 事务 T_i 对数据 A 解锁

caption: 用锁

加锁未必能保证正确性（因此需要不同的协议，来约定其用法）

锁的类型

排他锁X (exclusive locks)：只有一个事务能读、写，其他任何事务都不能读、写
共享锁S (shared locks)：所有事务都可以读，但任何事务都不能写
更新锁U (Update locks)：初始读，以后可升级为写
增量锁I (Incremental lock)：增量更新(例如A=A+x)，区分增量更新和其他类型的更新

caption: 相容性矩阵

封锁协议的 加锁时机

0-LP：有写要求时加排他锁，不再访问后后立即解锁
- 可防止：丢失修改
- 允许：脏读，重复读
1-LP：有写要求时加排他锁，事务提交后解锁
- 可防止：丢失修改，脏读
- 允许：重复读
2-LP：对于写，与 1-LP 一样。对于读：有读要求时加锁，不再访问后立即解锁
- 可防止：丢失修改、脏读、重复读
3-LP：对于读、写，有要求时加锁，事务提交后解锁
- 可防止：所有不一致性，包括幻读

caption: 封锁协议加锁时机

SQL的 隔离性级别

读未提交(read uncommitted) —相当于0级协议
读已提交(read committed) —相当于1级协议
可重复读(repeatable read) —相当于2级协议
可串行化(serializable) —相当于3级协议

封锁协议额 封锁粒度 (LOCKING GRANULARITY)

粒度单位：属性值 -> 元组 -> 元组集合 -> 整个关系 -> 整个DB
某索引项 -> 整个索引
靠前的: 并发度小，封锁开销小；
靠后的: 并发度大，封锁开销也大。

caption: 两段封锁协议

两段封锁协议(2PL: two-Phase Locking protocal)

读写数据前都加锁
每个事务分为两个阶段：加锁段，解锁段。加锁段不能有解锁操作，解锁段不能有加锁操作
- 用大白话描述就是，同一事务不能出现 “加锁、解锁、加锁” 这种顺序，（不分属性）

两段封锁协议可以保证冲突串行性

用归纳法证明：
1 个事务必然冲突可串行
假设 i 个事务冲突可串行，那么可证明 i + 1 个事务也冲突可串行

两段封锁协议可能产生死锁

基于时间戳的并发控制

基于时间戳的并发控制算法 基于若干时间戳的大小判断，强制使一组并发事务等价于串行执行

盘点有哪些冲突

读-读：无冲突
读-写，写-读：如果先执行的事务（时间戳早）先执行操作，那么无冲突。如果先执行的事务，后执行操作，那么有冲突
写-写：同上

基于时间戳的调度算法1

对数据表的每个元素，保留最大的时间戳
- RT(x) 读 x 的最大时间戳
- WT(x) 写 x 的最大时间戳
事务 T 的时间戳 TS
若 T 读 x，则比较 TS 与 WT(x)
- 若 TS >= WT(x)，则允许操作，并更新 RT(x) = max(RT(x), TS)
- 否则，有冲突，回滚，重启 T
若 T 写 x，则比较 TS 与 RT(x)，并且比较 TS 与 WT(x)
- 若 TS >= RT(x) and TS >= WT(x)，则允许操作，并更新 WT(x) = TS
  - 解释：比较 RT 以规避写-读冲突，比较 WT 以规避写-写冲突
- 否则，有冲突，回滚，重启 T，并且给 T 一个更大的时间戳

caption: 基于时间戳的调度算法1

基于时间戳的调度算法1 评价：

可以处理过晚的读、过晚的写
由于未判断回滚的情况，无法处理带回滚的冲突，例如脏读

托马斯写规则（Thomas Write Rule）

观察到，在写-写冲突中，在一些情况下，其实不必做撤销操作
什么情况呢？TS < WT(x)，也就是说，T 决定写入时，发现某个逻辑上更晚的事务已经写过 x。这意味着，T 要写入的数据已“过时”，不必要写入了。
因此不必撤销事务，只需要忽略这次写操作

完整的托马斯写规则

事务 T 准备写 x
1. 若 TS(T) < RT(x)
       撤销并重启 T

2. 否则，若 TS(T) < WT(x)
       忽略本次写操作

3. 否则
       执行写操作
       WT(x) = TS(T)

注意，托马斯写规则，也无法处理带撤销的情况

基于时间戳的调度算法2 为了处理带撤销的情况

对于每个数据元素 x，保留最大的时间戳：
- RT(x) 读 x 的最大时间戳
- WT(x) 写 x 的最大时间戳
- C(x) x 的提交位，boolean 类型。其为真，当且仅当最近写 x 的事务已经提交。
事务 T 的时间戳 TS

调度规则

如果 T 请求读
- 如果 TS >= WT(x)，此次读是可以实现的
  - 如果 C(x) 为真，同意请求，并且置 RT(x) = max(RT(x), TS)
  - 如果 C(x) 为假，等待，直到 C(x) 为真，或者写 x 的事务终止。（脏读）
- 如果 TS < WT(x)，回滚 T，并重启。（过晚的读）
如果 T 请求写
- 如果 TS >= RT(x) and TS(T) >= WT(x), 此写是事实上是可实现的
  - 同意执行，并且置 WT(x) = TS; C(x) = False
- 如果 TS >= RT(x) and TS < WT(x)，此写是事实上可实现的。但x已经有一个更晚的值
  - 如果 C(x) 为真，那么前一个x的写已提交；则忽略T的写；继续执行。(托马斯写规则)
  - 如果 C(x) 为假，则推迟T，直到 C(x) 为真或写x的事务终止。
- 如果 TS(T) < RT(x), 此写是事实上不可实现的，T必须回滚。(过晚的写)
如果 T 提交
- 找到 T 所写的所有元素 x，并全部置 C(x) = True
- 唤醒所有等待 x 被提交的事务，允许它们继续执行
如果 T 回滚
- 撤销并恢复所有的 x（这要求系统有旧版本信息，或者 undo log）
- 唤醒所有等待 x 的事务，并置 C(x) = True
- 重启 T，并给它分配一个更大的时间戳

基于有效性确认的并发控制

基于时间戳的并发控制，其回滚的次数太多。

基于有效性确认的并发控制 思路：

每个事务在启动时赋予时间戳
对于每个活跃事务，维护其读数据的集合 RS(T)，写数据的集合 WS(T)
- 通过对不同事务的读写集合做判断算法，判断其是否冲突（有效性确认）
- 以此完成事务的提交与回滚，使其等价于串行执行
事务分为三个阶段：
- 读阶段。事务从数据库读取 RS(T) 中的所有元素。这个阶段在其局部地址空间计算其将要写出的值
- 有效性确认阶段。调度器通过比较该事务与其它事务的读写集合来确认该事务的有效性
- 写阶段。事务往数据库中写入其写集合中元素的值。
调度器维护三个集合：
- START集合。已经开始但尚未完成有效性确认的事务集合。对此集合中的事务，调度器维护 START(T)，即事务T开始的时间戳。
- VAL集合。已经确认有效性但尚未完成第3阶段写的事务。对此集合中的事务，调度器维护 START(T) 和 VAL(T)（T确认的时间）。
- FIN集合。已经完成第3阶段的事务。对这样的事务T, 调度器记录 START(T), VAL(T) 和 FIN(T)（T完成的时间）。

有效性确认规则

冲突一：一个较早的事务U现在正在写入T应该读过的某些对象，则T的有效性不能确认（存在冲突）
判断条件：

U in VAL | FIN, 即U已经过有效性确认。
FIN(U) > START(T), 即U在T开始前没有完成。
RS(T) | WS(U) 非空, 特别地，设其均包含数据库元素为x。

则T和U的执行存在冲突，T不应进行有效性确认

冲突二：T在有效性确认后可能比一个较早的事务先写某个对象，则T的有效性不能确认（存在冲突）
判断条件：

U in VAL。即U的有效性已经确认
FIN(U) > VAL(T), 即U在T进入其有效性确认阶段以前没有完成。
WS(T) ∩ WS(U) 非空, 特别地，设其均包含数据库元素x。

则T和U的执行存在冲突，T不应进行有效性确认

caption: 基于有效性确认的冲突规则

故障恢复

故障恢复涉及到如何保证 原子性 和 持久性

有哪些故障？

事务故障
- 某一个程序(事务)自身运行错误所引起的故障
- 影响该程序(事务)本身
系统故障
- 由于掉电、非正常关机等所引起的故障
- 影响正在运行的事务以及数据库缓冲区, 数据库缓冲区将涉及正在运行和已经运行的事务
介质故障
- 由于介质损坏等所引起的故障
- 影响是全面的，既影响内存中的数据, 又影响介质中存储的数据

对于系统故障：使用 运行日志（System Log）

检查点：在这个时刻，强制缓冲区（内存）中的所有内容写回到磁盘
故障恢复：从检查点开始，把所有日志运行一遍
- 检查点之前已经结束的事务不需要恢复
- 检查点之后、故障点之前结束的事务：重做事务（Redo）
- 故障点还未结束的事务：撤销事务（Undo）

对于介质故障使用副本（Copy）

在某一时刻（叫做 转储点），对数据库在其它介质存储上产生另一份等同记录。
故障恢复
- 先用副本替换被损坏的数据库（恢复到转储点）
- 再用日志恢复到故障点
备份周期的确定：过频，影响性能。过疏，运行日志过大（必须保留转储点之后的所有日志），也影响性能。

caption: 故障时间序列

事务有哪些操作？

每个事务的读/写某些元素
- READ(X,t)：将元素X读到事务的局部变量t中
- WRITE(X,t)：将事务局部变量t写回元素X
- INPUT(X)：将元素X从磁盘读入到内存缓冲区中
- OUTPUT(X)：将元素X写回到磁盘中
每个事务都以提交或者撤销结束
- COMMIT：事务提交
- ABORT：事务撤销

缓冲区处理策略

Force：内存中的数据最晚在commit的时候写入磁盘。
No steal：不允许在事务commit之前把内存中的数据写入磁盘。
No force：内存中的数据可以一直保留，在commit之后过一段时间再写入磁盘。
- 在系统崩溃的时候可能还没写入到磁盘，需要Redo
Steal：允许在事务commit之前把内存中的数据写入磁盘。
- 此时若系统在commit之前崩溃时，已经有数据写入到磁盘了，要恢复到崩溃前的状态，需要Undo

日志记录哪些信息？

<Start T>，表示事务T已经开始
<Commit T>，表示事务T成功完成
<Abort T>，事务T未成功，被中止
<T, X, v_old>（Undo 型日志）或者 <T, X, v_new>（Redo 型日志）或者 <T, X, v_old, v_new>（Undo/Redo 型日志）

三种类型的运行日志：

Undo型日志
Redo型日志
Undo/Redo型日志

caption: 读写性能和日志策略

Undo型日志

记录 <T, X, v_old>
OUTPUT(X)
记录 <Commit T> 或 <Abort T>

使用 Undo 型日志进行故障恢复

确定每个事务是否已完成
- 含有 <Start T>、<Commit T>：已完成
- 含有 <Start T>、<Abort T>：未完成
- 仅含有 <Start T>：未完成
日志尾部开始反序，直到检查点结束
- <Commit T>：标记 T 已完成
- <Abort T>：标记 T 结束未完成
- <T, X, v_old>：如果 T 未完成，将 v_old 写回到磁盘；否则跳过
- <Start T>：跳过

关于检查点

静止检查点，是周期性定时设置的
- 停止接受新的事务，并等待当前所有事务提交或终止，并记录相关日志
- 将日志刷新到磁盘，写入 <CKPT>
非静止检查点，触发时不必关闭系统，允许新事务进入
- 写入一条 <START CKPT(T1, …, Tk)>
- 其中的 T1, ..., Tk 是所有活跃的未结束的事务
- 系统继续正常运行，直到 T1, ..., Tk 都完成，然后写入 <END CKPT>
- 对于非静止检查点，Undo 时恢复到 <START CKPT(T1, …, Tk)>

Redo 型日志

写入 <T, X, x_new>
写入 <Commit T>
OUTPUT(X)（注意，Undo 这一步是在第二步，有所不同）

使用 Redo 型日志进行故障恢复

确定每个事务是已经完成
- 含有 <Start T>、<Commit T>：已完成
- 含有 <Start T>、<Abort T>：未完成
- 仅含有 <Start T>：未完成
从日志启始位置正序处理：
- <Commit T>：标记 T 已完成
- <Abort T>：标记 T 结束未完成
- <T, X, v_new>：如果 T 已完成，则把 v_new 写回到磁盘；否则跳过；
- <Start T>：跳过

检查点，与 Undo 一样，也分为静态检查点、动态检查点，规则一样。

对于静态检查点，与 Redo 一样
对于动态检查点，查找最后一个 <END CKPT>，从其对应 <START CKPT> 开始 Redo

Undo/Redo 型日志

为什么？

Undo 性能低（频繁写磁盘）
Redo 灵活性差（必须 Commit 后才写入）

写入顺序

写入 <T, X, v_old, v_new>
<Commit T> 写入日子
OUTPUT(X)
- 其中第 2 步和第 3 步可以交换

使用 Undo/Redo 型日志进行故障恢复

确定每个事务是否已经完成
- 含有 <Start T>、<Commit T>：已完成
- 含有 <Start T>、<Abort T>：未完成
- 仅含有 <Start T>：未完成
从前往后， Redo 所有已提交的事务；然后从后往前，Undo 所有未完成事务的修改

参考资料

哈尔滨工业大学：数据库系统【上】：模型与语言、【中】：建模与设计、【下】：管理与技术

课程PPT备份：https://github.com/codes-books/database

陆军工程大学：数据库原理与应用 https://www.icourse163.org/course/PAEU-1003647009