❤️ 1526

0x00_读论文 8

0x11_算法平台 15

0x12_Pandas与numpy 12

0x13_特征工程 4

0x21_有监督学习 21

0x23_深度学习 7

0x24_NLP 13

0x25_CV 11

0x26_torch 11

0x31_降维 10

0x32_聚类 5

0x33_图模型 9

0x41_统计模型 9

0x42_概率论 7

0x43_时间序列 10

0x44_随机过程 2

0x51_代数与分析 15

0x52_方程 2

0x53_复分析与积分变换 8

0x55_数值计算 7

0x56_最优化 11

0x58_密码学 12

0x59_应用数学 9

0x60_启发式算法 8

0x70_可视化 13

0x80_数据结构与算法 17

0xa0_蒙特卡洛方法 6

0xb0_Python语法 18

0xd0_设计模式 6

经济学知识补漏

道格拉斯生产函数

$Y=AL^\alpha K^{1-\alpha}$
可以证明：

  • 规模报酬不变
  • 劳动收入的占比是$\alpha$

货币需求函数

传统

$PV=MY$

这里有个题目： 在W国，货币流通速度不变，实际GDP增长时5%，货币存量增长14%，名义利率是11%，实际利率是多少？
先把数量方程写出变化的形式（微分），求出通胀率。

剑桥

$M=kPY$

凯恩斯

$L=L_1(Y)+L_2(i)$
where,

  • $L_1$是交易动机和预防动机，是Y的增函数
  • $L_2$是投机动机，是i的减函数

弗里德曼

$M=f(P,r_b,r_c,1/P \cdot dP/dt,w,y,u)$
where,

  • $M$是名义货币量
  • $P$是价格水平
  • $r_b$是债券预期收益率
  • $r_c$是股票预期收益率
  • $1/P \cdot dP/dt$是物价预期变化率
  • $w$是人力财富与非人力财富比率
  • $y$是货币收入
  • $u$是其它随机因素

通胀带来的成本

  • 鞋底成本。频繁去银行
  • 菜单成本。企业频繁改价
  • 相对价格变动成本。引起配置无效率
  • 税收扭曲。通胀提高税收负担
  • 生活不方便。因为货币作为计量尺度总是在变化，造成不便。
  • 任意再分配财富。

就业

效率工资
解释失业第三个理论（其它2个是最低工资法、工会）。认为企业为了促进生产率提高，会付出比劳动力市场出清更高的工资，以保证效率提高。结果是一方面提高工资水平，降低劳动需求；另一方面提高效率，降低劳动需求。

Solow growth model 1: 资本累积和人口增长

核心方程

  1. 资本存量：投资和折旧使资本存量变化
    • $\Delta k=i-\delta k$
    • $i=sf(k)$
    • 其中，$i$时投资,$s$是储蓄率，$\delta$是折旧率
    • 合起来，就是$\Delta k=sf(k)-\delta k$
  2. 索罗模型核心方程
    • 人均产出$y=f(k)$
    • 人均消费$c=(1-s)f(k)$

核心方程的解

1. 稳态

$\Delta k=0$

2. 资本的黄金律水平

满足$\max c$的人均资本水平

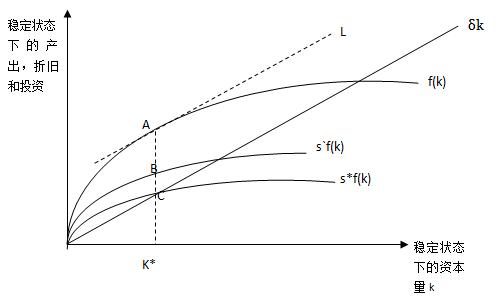
3. 人口自然增长

加入人口增长因素后（但科技增长仍然不变），假设人口增长率为$n$

资本运动方程变成$\Delta k=i-(\delta+n) k$
由此得出资本的稳态。【试试画一个类似上面的图】
然后进一步的结论是，如果人口增长变高，稳态的人均资本和人均收入都减少。

有人口增长的黄金律是$c=y-i=f(k)-(\delta_n)k$

Solow growth model 2: 技术、经验进步和政策

劳动效率提升

$Y=F(K,LE)$
where，

  • $LE$是效率工人数量，$E$是效率，
  • 假设劳动效率增长率不变，$g=dE/E$

核心方程是效率工人人均的形式： $\delta k=sf(k)-(\delta +n+g)k$
其中定义$k=K/(LE),y=Y/(LE)$
结论是，稳态下，$k,y$不变，$Y/L$增长率为g，$Y$增长率为$n+g$

两部门模型

制造业生产函数$Y=F[K,(1-u)LE]$
大学生产函数$\delta E=g(u)E$
资本累积$\Delta K=sY-\delta K$

其中，

  • $u$是大学的劳动力比例，$1-u$是制造业劳动比例
  • $E$是知识存量，$g(u)$是知识增长率取决于大学的劳动力比例

经济增长源泉的核算

$Y=AF(K,L)$